A small block of mass m is kept on the inclined surface of a wedge of mass M. The inclined surface of the wedge makes an angle θ with the horizontal. The wedge is kept on a frictionless rigid horizontal floor. You can neglect friction between the block and the wedge also. An external agent applies a horizontal force F on the wedge.
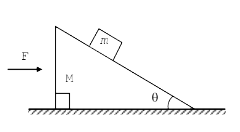
The value of the force F so that the wedge remains at rest is F1. Which of the options is incorrect?
When F=F2, the force with which wedge presses on the floor is less than its value in the case when F=F1
F>F1
F2 depends on the mass of wedge M
The contact force between the block and the wedge is greater than the weight of the block
The correct Answer is:A
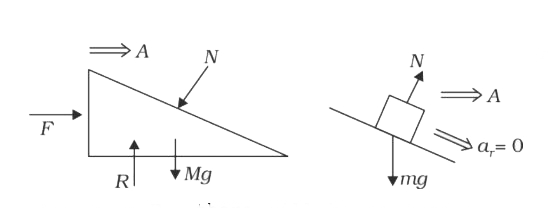
mgsinθ=m(Acosθ+ar)⇒A=gtanθ
F2=(m+M)A=(M+m)gtanθ
Ncosθ=mg⇒N=mg/cosθ
R=Mg+Ncosθ=Mg+mg
Similar Questions
A block of mass m is placed on the inclined sufrace of a wedge as shown in fig. Calculate the acceleration of the wedge and the block when the block is released. Assume all surfaces are frictionless.

View SolutionA wedge of mass M makes an angle θ with the horizontal. The wedge is placed on horizontal frictionless surface. A small block of mass m is placed on the inclined surface of wedge. What horizontal force F must be applied to the wedge so that the force of friction between the block and wedge is zero ?
View Solution
Knowledge Check
A small block of mass m is kept on the inclined surface of a wedge of mass M. The inclined surface of the wedge makes an angle θ with the horizontal. The wedge is kept on a frictionless rigid horizontal floor. You can neglect friction between the block and the wedge also. An external agent applies a horizontal force F on the wedge.

The value of the force F so that the wedge remains at rest is F1. Which of the options is incorrect?AF4=F1BF4=F2CF4=F2DF4 depends on μsIn fig. mass m is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.
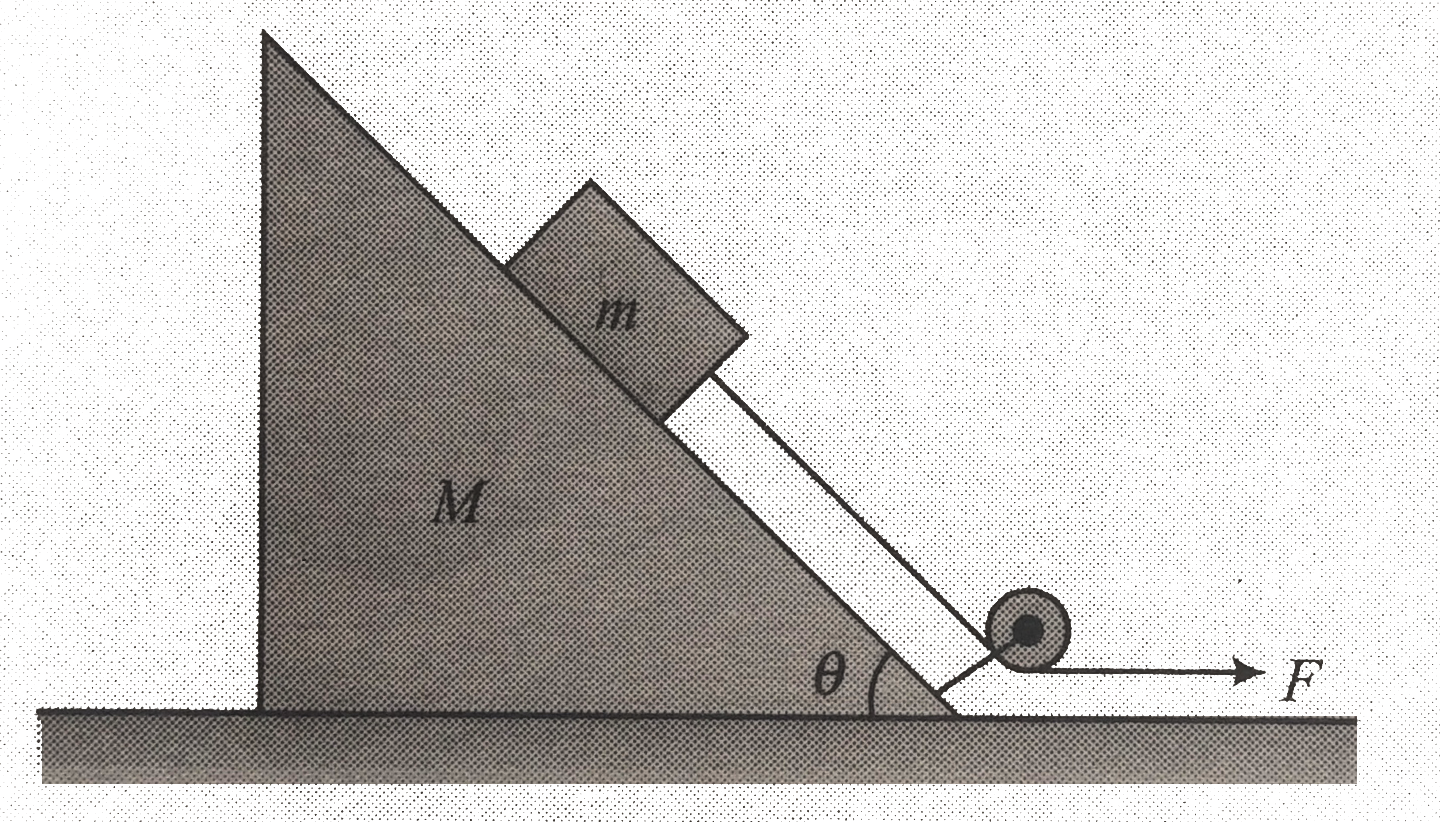 Aa=F(1−cosθ)mg2sinθcosθM+2msin2θBa=F(1+cosθ)+mgsinθcosθM+msin2θCa=F(1−cosθ)−mgsinθcosθM+msin2θDa=F(1+cosθ)−mgsinθcosθM−msin2θ
Aa=F(1−cosθ)mg2sinθcosθM+2msin2θBa=F(1+cosθ)+mgsinθcosθM+msin2θCa=F(1−cosθ)−mgsinθcosθM+msin2θDa=F(1+cosθ)−mgsinθcosθM−msin2θA small block of mass m is kept on a rough inclined surface of inclination θ fixed in an elevator. The elevator goes up with a uniform velocity v and te block does not slide n te wedge. The work done by the force of friction on the block in time t will be
AzeroBmgvtcos2θCmgvtsin2θDmgvtsin2θ
A wedge with mass M rests on a frictionless horizontal surface A block with mass m is placed on the wedge. There is no friction between the block and the wedge. A horizontal force f is applied to the wedge. What magnitude F must have if the block is to remain at constant height above the table top?

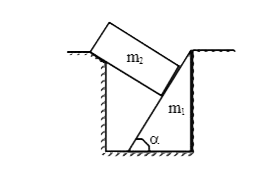
View SolutionA wedge of mass m1and a block of mass m2are in equlibrium as shown. Inclined surface of the wedge has an inclination α with the horizontal. Each surface is frictionless. The noram reaction on the wedge may be -
View SolutionA block of mass m is placed on a smooth wedge of inclination θ. The while system is acceleration horizontally so that the block does not slip. Find (a) horizontal acceleration, (b) normal force between the block and the wedge and (c) the horizontal force applied on the wedge.
View SolutionA block of mass m is kept on an inclined plane of mass 2m and inclination α to horizontal. If the whole system is accelerated such that the block does not slip on the wedge then :
View SolutionA block of mass 2kg slides down the face of a smooth 45∘ wedge of mass 9kg as shown in the figure. The wedge is placed on a frictionless horizontal surface. Determine the acceleration of the wedge.

View Solution
