A particle of mass 0.2 kg has an intial speed of at the bottom of a rough inclined plane of inclination and vertical height 0.5 m . What is the speed of the particle as it reaches the top of the inclined plan ? (Take ) .
AB = 1m
Let f be the force of friction
Net downward force along the plane on the particle moving up the plane is

Retaradation of particle
Let v be the velocity of particle at top
Then as
V = 2.24m/s
Similar Questions
A particle is projected from the bottom of an inclined plane of inclination 30∘ with velocity of 40m/s at an angle of 60∘ with horizontal. Find the speed of the particle when its velocity vector is parallel to the plane. Take g=10m/s2.
View SolutionA block of mass 10 kg rests on a rough inclined plane of inclination 45∘ with the horizontal. What minimum force is required to just move the block up the inclined plane. Given μs=0.5andg=10ms−2.
View Solution
Knowledge Check
A disc of mass 3 kg rolls down an inclined plane of height 5 m. The translational kinetic energy of the disc on reaching the bottom of the inclined plane is
A50 JB100 JC150 JD175 JA cylinder of mass 2 kg is released from rest from the top of an inclined plane of inclination 30∘ and length 1m. If the cylinder rolls without slipping, then its speed when it reaches the bottom, is [Take, g = 10 m/s2]
A203 m/sB√203 m/sC103 m/sD√103 m/sA block is projected upwards with a velocity of 5 m/s from the bottom of a rough inclined plane of inclination 30° with the horizontal. It stops after 0.5 s. What is the coefficient of friction ? (g=10m/s2)
A√3B1√3C√2D√5
A particle of mass 0.1kg has an iniital speed of 4ms−1 at a point A on a roudh horizontal road. The coefficient of friction between the object and road is 0.15. The particle moves to a point B at a distance of 2m from A. What is the speed of particle at B ?
Take g=10ms−2
View SolutionA body of mass 10kg is lying on a rough inclined plane of inclination 37∘ and μ=1/2 , the minimum force required to pull the body up the plane is
View SolutionA wooden box of mass 8kg slides down an inclined plane of inclination 30∘ to the horizontal with a constant acceleration of 0.4ms−2 What is the force of friction between the box and inclined plane ? (g=10m/s2) .
View SolutionA ball is projected from the bottom of an inclined plane of inclination 30∘, with a velocity of 30ms−1, at an angle of 30∘ with the inclined plane. If g=10ms−2 , then the range of the ball on given inclined plane is
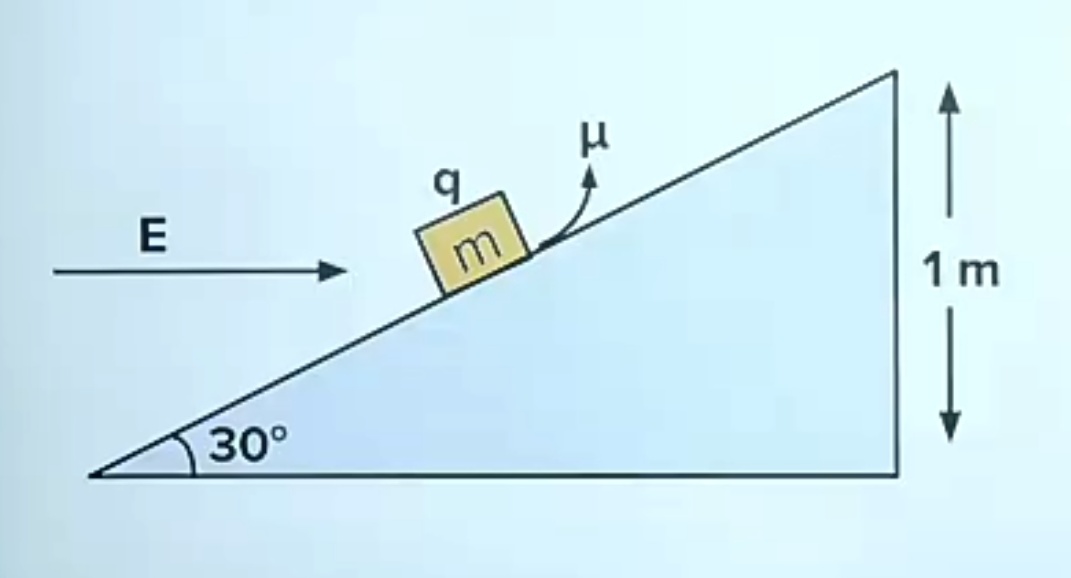
View SolutionFind the time taken by the block to reach the bottom of inclined plane. E=200ˆi N/C , M=1kg ,q=5mC,g=10ms2 μ=0.2
View Solution
