The initial speed of a bullet fired from a rifle is 630 m/s. . The rifle is fired at the centre of a target 700 m away at the same level as the target. How far above the centre of target, the rifle must be aimed in order to hit the target?
6.1 m
1.0 m
9.8 m
4.2m
The correct Answer is:A
To solve the problem, we need to determine how far above the center of the target the rifle must be aimed in order to hit the target. The bullet is fired with an initial speed of 630 m/s at a target that is 700 m away.
1. Identify the Given Values:
- Initial speed of the bullet, u=630m/s
- Distance to the target, R=700m
- Acceleration due to gravity, g=10m/s2 (approximate value)
2. Use the Range Formula:
The range R of a projectile is given by the formula:
R=u2sin(2θ)g
Rearranging this formula to find sin(2θ):
sin(2θ)=R⋅gu2
3. Substitute the Known Values:
Substitute R=700m, g=10m/s2, and u=630m/s into the equation:
sin(2θ)=700⋅106302
Calculate 6302:
6302=396900
Now substitute:
sin(2θ)=7000396900≈0.0176
4. Calculate 2θ:
To find 2θ, take the inverse sine:
2θ=arcsin(0.0176)
Using a calculator, we find:
2θ≈1.01∘
Therefore, θ≈0.505∘.
5. Calculate the Height H:
We know that:
tan(θ)=HR
Rearranging gives:
H=R⋅tan(θ)
Using R=700m and tan(θ)≈sin(θ) for small angles:
tan(0.505∘)≈0.0088
Thus:
H=700⋅0.0088≈6.16m
6. Final Result:
The rifle must be aimed approximately H≈6.16m above the center of the target to hit it.
Summary:
The rifle must be aimed approximately 6.16 meters above the center of the target.
- Initial speed of the bullet, u=630m/s
- Distance to the target, R=700m
- Acceleration due to gravity, g=10m/s2 (approximate value)
The range R of a projectile is given by the formula:
R=u2sin(2θ)g
Rearranging this formula to find sin(2θ):
sin(2θ)=R⋅gu2
Substitute R=700m, g=10m/s2, and u=630m/s into the equation:
sin(2θ)=700⋅106302
Calculate 6302:
6302=396900
Now substitute:
sin(2θ)=7000396900≈0.0176
To find 2θ, take the inverse sine:
2θ=arcsin(0.0176)
Using a calculator, we find:
2θ≈1.01∘
Therefore, θ≈0.505∘.
We know that:
tan(θ)=HR
Rearranging gives:
H=R⋅tan(θ)
Using R=700m and tan(θ)≈sin(θ) for small angles:
tan(0.505∘)≈0.0088
Thus:
H=700⋅0.0088≈6.16m
The rifle must be aimed approximately H≈6.16m above the center of the target to hit it.
The rifle must be aimed approximately 6.16 meters above the center of the target.
Similar Questions
When a rifle is fired at a distant target, the barrel is not lined up exactly on the target. Why ?
View SolutionA bullet with muzzvelocity 100 m/s is to be shot at a target 30 m away in the horizontal line .How high above the target must the renaimed so that the bullet will hit the target?

View Solution
Knowledge Check
A bullet with muzzle velocity 100ms−1 is to be shot at a target 30m away in the same horizontal line. How high above the target must the rifle be aimed so that the bullet will hit the target ?
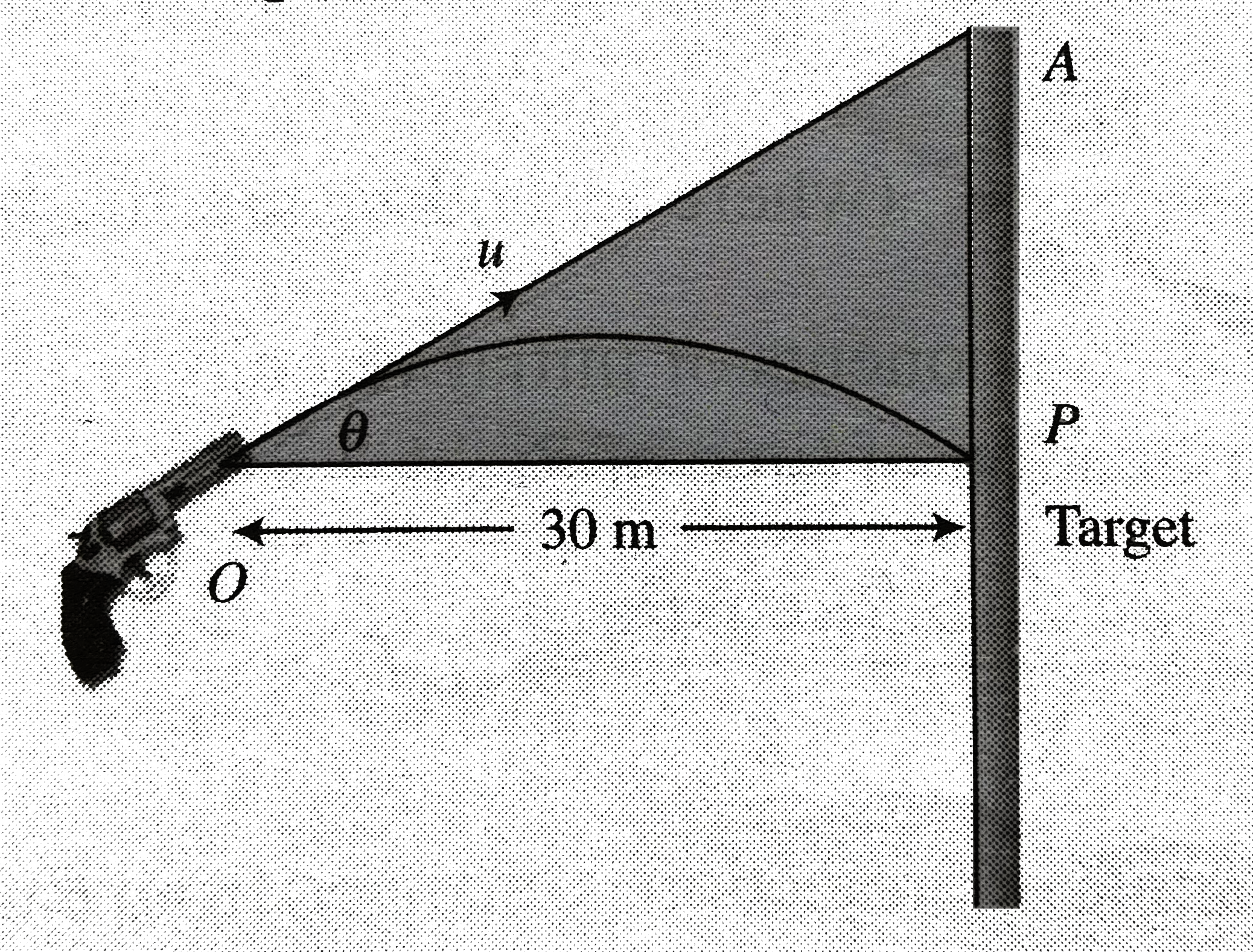 .A0B0.45cmC45cmD90cm
.A0B0.45cmC45cmD90cmA rifle shoots a bullet with a muzzle velocity of 400ms−1 at a small target 400m away. The height above the target at which the bullet must be aimed to hit the target is (g=10ms−2).
A1 mB5 mC10 mD0.5 mA bullet fired from a rifle travels at an average speed of 2520 km/hr. It hits the target after 0.2 seconds. How far (in metre) is the target from the rifle?
A70B140C100D200
A rifle that shoots bullets at 460 m/s is to be aimed at a traget 45.7 m away. If the center of the target is level with the rifle, how high above the target must the rifle barrel be pointed so that the bullet hits dead center?
View SolutionA bullet is fired aiming target as shown. If the target is dropped from rest at the same time then prove that it will hit to target.

View SolutionA bullet fired from a rifle attains a maximum height of 5 m and crosses a range of 200 m. Find the angle of projection.
View SolutionA bullet fired from a rifle travels at an average speed of 2520 km/hr. It hits the target after 0.2 seconds. How far (in m) is the target from the rifle ?
View SolutionA gun fires a bullet at a speed of 140ms−1.If the bullet is to hit a-target at the same level as the gun and at 1km distance, the angle of projection may be
View Solution

