A particle is prjected up an inclined with initial speed v=20m/s at an angle θ=30∘ with the plane. The component of its velocity perpendicular to the plane when it strikes the plane is:
The correct Answer is:5
Component of velocity perpendicular to the plane an landing = component of velocity perpendicular to the plane at the point of projection =20sin30∘=10m/s.
Similar Questions
In the above problem, what is the component of its velocity perpendicular to the plane when it strikes at A ?
View SolutionAn inclined plane makes an angle θ0=30∘ with the horizontal. A particle is projected from this plane with a speed of 5ms−1 at an angle of elevation β=30∘ with the horizontal as shown in (Fig. 5.53).
(a) Find the range of the particle on the plane when it strikes the plane.
(b) Find the range of the particle for β=120∘.
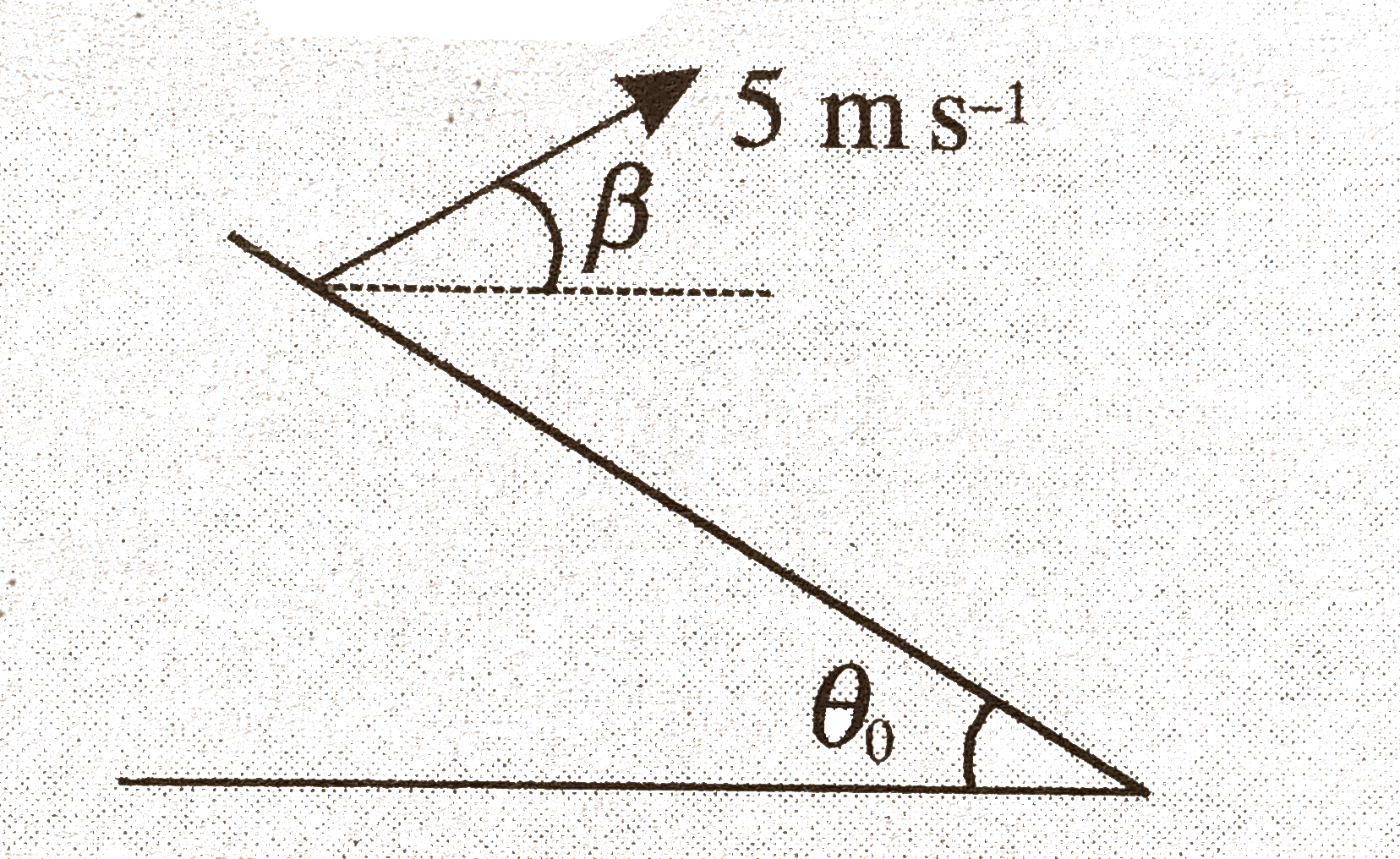 .
.
View Solution
Knowledge Check
A particle is projected up an inclined plane with initial speed v=20m/s at an angle θ=30∘ with plane. The component of its velocity perpendicular to plane when it strikes the plane is
A10√3m/sB10m/sC5√3m/sDData is insufficientA plane is inclined at an angle 30∘ with horizontal. The component of a vector →A=−10k perpendicular to this plane is: (here z-direction is vertically upwards)
A5√2B5√3C5D2.5A particle is projected up with a velocity of v0=10m/s at an angle of θ0=60∘ with horizontal onto an inclined plane. The angle of inclination of the plane is 30∘. The time of flight of the particle till it strikes the plane is (take g=10ms−2)
A1sB1/2sC2√3sD12√3s
A particle is projected up an inclines plane. Plane is inclined at an angle θ with horizontal and particle is projected at an angle α with horizontal. If particle strikes the plane horizontally prove that tanα=2tanθ
View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA particle is projected horizontal with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane?
View SolutionThe ratio of component of velocity striking perpendicular to the plane for upward and downward projection is:
View SolutionA small ball is projected up a smooth inclined plane with an initial speed of 10m/s along the direction at 30∘ to the bottom edge of the slope. It returns to the edge after 2s. The ball is in constant with the inclined plane throughout the process. What is the inclination angle of the plane?
View Solution