The range of a rifle bullet on level ground is 60 m. The range (in m) upon incline of 30∘ is . (Take g=10m/s2)
The correct Answer is:720
To solve the problem, we need to find the range of a rifle bullet fired at an incline of 30∘ given that its maximum range on level ground is 60m. We will use the equations of projectile motion to derive the solution step by step.
Step 1: Understand the relationship between range, initial velocity, and angle
The range R of a projectile launched with an initial velocity u at an angle θ is given by the formula:
R=u2sin(2θ)g
where g is the acceleration due to gravity.
Step 2: Find the initial velocity u
Given that the maximum range on level ground is 60m at an angle of 45∘, we can use the range formula:
60=u2sin(90∘)g
Since sin(90∘)=1, this simplifies to:
60=u2g
Substituting g=10m/s2:
60=u210
Multiplying both sides by 10:
u2=600
Step 3: Calculate the range at 30∘
Now we need to find the range R1 when the projectile is launched at an angle of 30∘:
R1=u2sin(2×30∘)g
Calculating sin(60∘):
sin(60∘)=√32
Substituting u2 and g into the range formula:
R1=600⋅√3210
This simplifies to:
R1=600√320=30√3
Step 4: Calculate the numerical value of the range
Now we can calculate 30√3:
Using √3≈1.732:
R1≈30×1.732=51.96m
Final Answer
Thus, the range of the rifle bullet upon incline of 30∘ is approximately 52m.
The range R of a projectile launched with an initial velocity u at an angle θ is given by the formula:
R=u2sin(2θ)g
where g is the acceleration due to gravity.
Given that the maximum range on level ground is 60m at an angle of 45∘, we can use the range formula:
60=u2sin(90∘)g
Since sin(90∘)=1, this simplifies to:
60=u2g
Substituting g=10m/s2:
60=u210
Multiplying both sides by 10:
u2=600
Now we need to find the range R1 when the projectile is launched at an angle of 30∘:
R1=u2sin(2×30∘)g
Calculating sin(60∘):
sin(60∘)=√32
Substituting u2 and g into the range formula:
R1=600⋅√3210
This simplifies to:
R1=600√320=30√3
Now we can calculate 30√3:
Using √3≈1.732:
R1≈30×1.732=51.96m
Thus, the range of the rifle bullet upon incline of 30∘ is approximately 52m.
Similar Questions
Knowledge Check
A ball is thrown upward with speed 10 m/s from the top to the tower reaches the ground with a speed 20 m/s. The height of the tower is [Take g=10m/s2]
A10 mB15 mC20 mD25 mA projectile is launched with a speed of an angle 60∘ with the horizontal from a sloping surface of inclination 30∘. The range R is: (g=10m/s2)
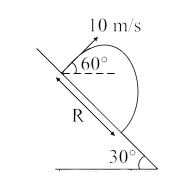 A4.9 mB13.3 mC9.1 mD12.6 m
A4.9 mB13.3 mC9.1 mD12.6 mThe time of flight of a projectile is 10 s and range is 500m. Maximum height attained by it is [g=10m/s2]
A25mB50mC82mD125m
A projectile is projected from ground with an initial velocity (5ˆi+10ˆj)m/s If the range of projectile is R m, time of flight is Ts and maximum height attained above ground is Hm, find the numerical value of R×HT. [Take g=10m/s2]
View SolutionA ball is projected from a point on an inclined plane horizontally. It takes 1√2 seconds to strike the plane. If the incline plane makes an angle of 30∘ with horizontal then find the range of the ball on incline plane in meters[g=10m/s2]
View SolutionWhat are the two angles of projection of a projectile projected with velocity of 30m/s, so that the horizontal range is 45m. Take, g=10m/s2.
View SolutionA ball is thrown at a speed of 40 m/s at an angle of 600 with the horizontal. Find a. the maximum height reached and b. the range of te ball. Take g=10ms2.
View SolutionA solid cylinder rolls down an inclined plane of height 3m and reaches the bottom of plane with angular velocity of 2√2rad/s. The radius of cylinder must be [take g=10m/s2]
View Solution

