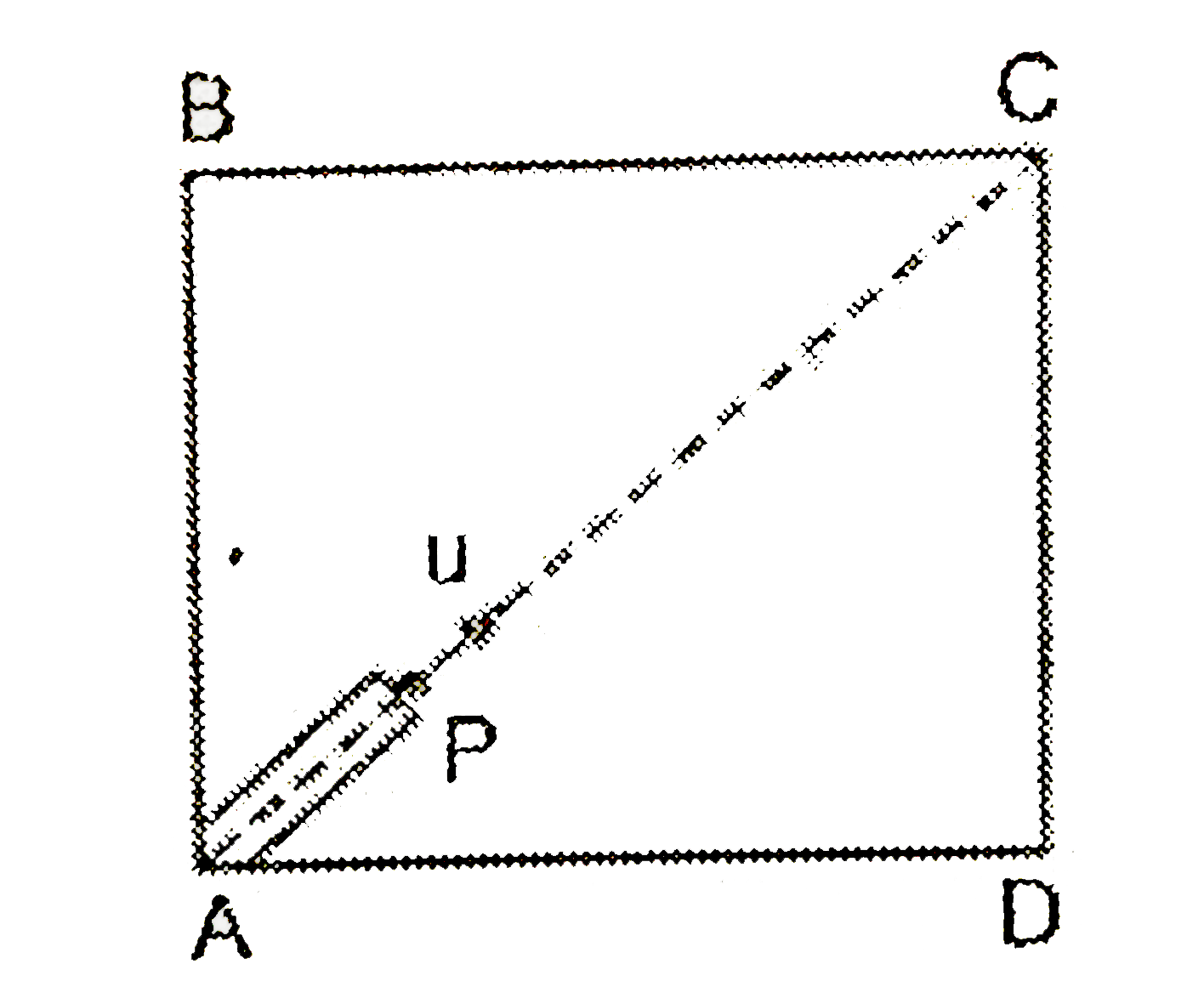
A large rectangular box ABCD falls vertically with an acceleration a. a toy gun fixed at A and aimed towards C fired a particle P.
P will hit C if a = g
P will hit the roof BC if a>g
P will hit the wall CD or the floor AD if a<g
May be either (A), (B) or (C), depending on the speed of projection of P
The correct Answer is:A, B, C
If the relative acceleration of bullet w.r.t. box is zero then its motion is straight line w.r.t. box vertical displacement will be different if a≠g.
Similar Questions
An earth satellite is revolving in a circular orbit of radius a with velocity υ0. A gun is the satellite and is aimed directly towards the earth. A bullet is fired from the gun with muzzle velocity υ02. Neglecting resistance offered by cossmic dust and recoil of gun, calculate maximum and minimum distance of bullet from the centre of earth during its subsequency motion.
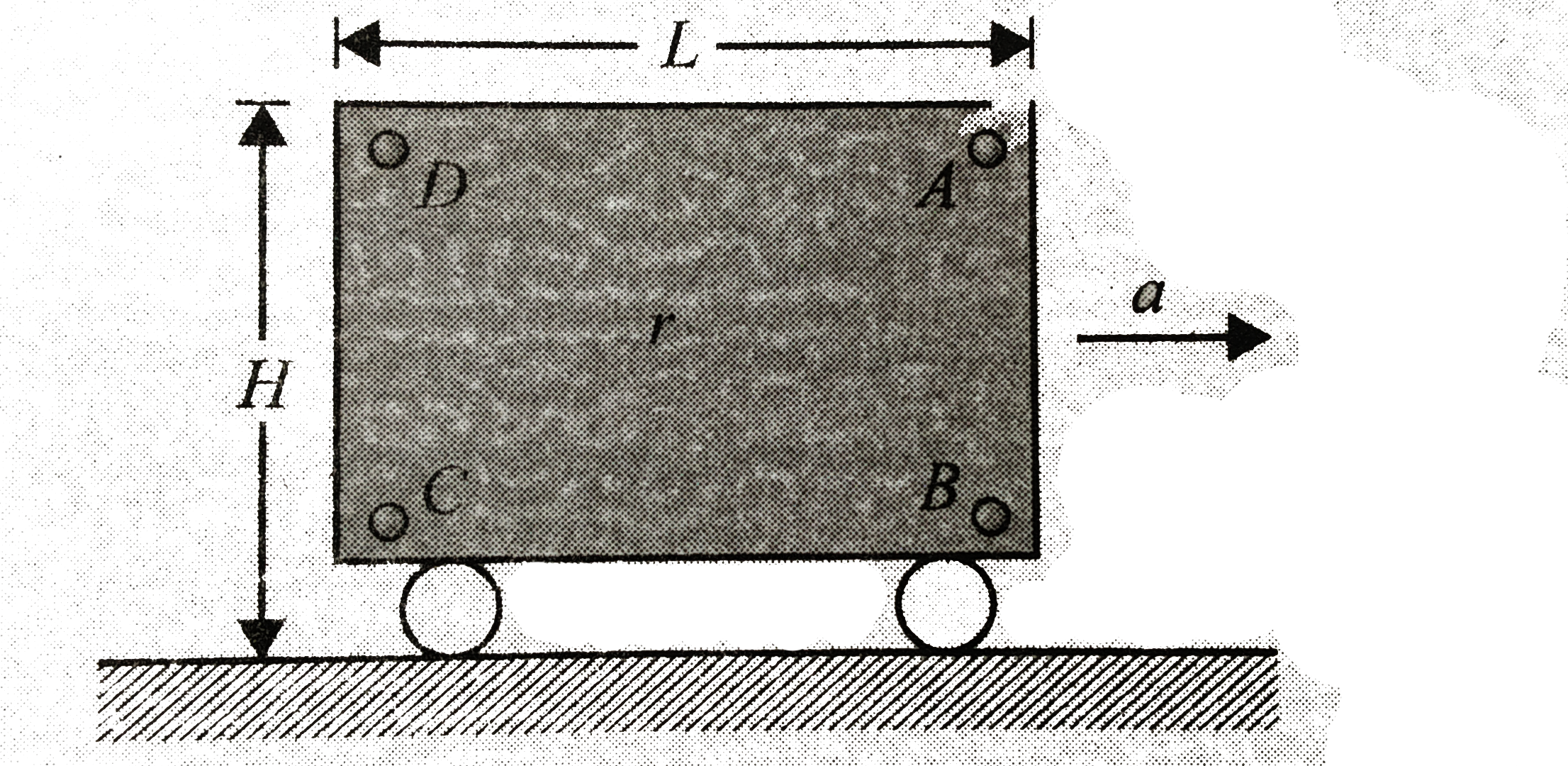
View SolutionA rectangular box is completely filled with a liquid of density ρ, as shown in Fig. The box is accelerated horizontally with a constant acceleration a. Determine the gauge pressures at the four points A,B,C and D.
View Solution
Knowledge Check
A large rectangular box moves vertically downward with an acceleration a. A toy gun fixed at A and aimed towards C fires a particle P.
 AP will hit C if a=gBP will hit the roof BC, if a>gCP will hit the CD if a<gDMay be either (a), (b) or (c) depending on the speed of projection of P.
AP will hit C if a=gBP will hit the roof BC, if a>gCP will hit the CD if a<gDMay be either (a), (b) or (c) depending on the speed of projection of P.A large box moves vertically downwards with an acceleration a. A toy gun fixed at A aimed towards C fires a particle P.
 AP will hit C if a=gBP will hit the roof BC, if fa>gCP will hit the wall CD if a<gDMay be either (A),(B) or (C), depending on the speed of projection of P.
AP will hit C if a=gBP will hit the roof BC, if fa>gCP will hit the wall CD if a<gDMay be either (A),(B) or (C), depending on the speed of projection of P.A large rectangular box has been rotated with a constant angular velocity ω1 about its axis as shown in the figure. Another small box kept inside the bigger box is rotated in the same sense with angular velocity ω2 about its axis (which is fixed to floor of bigger box). A particle P has been identified, its angular velocity about AB would be
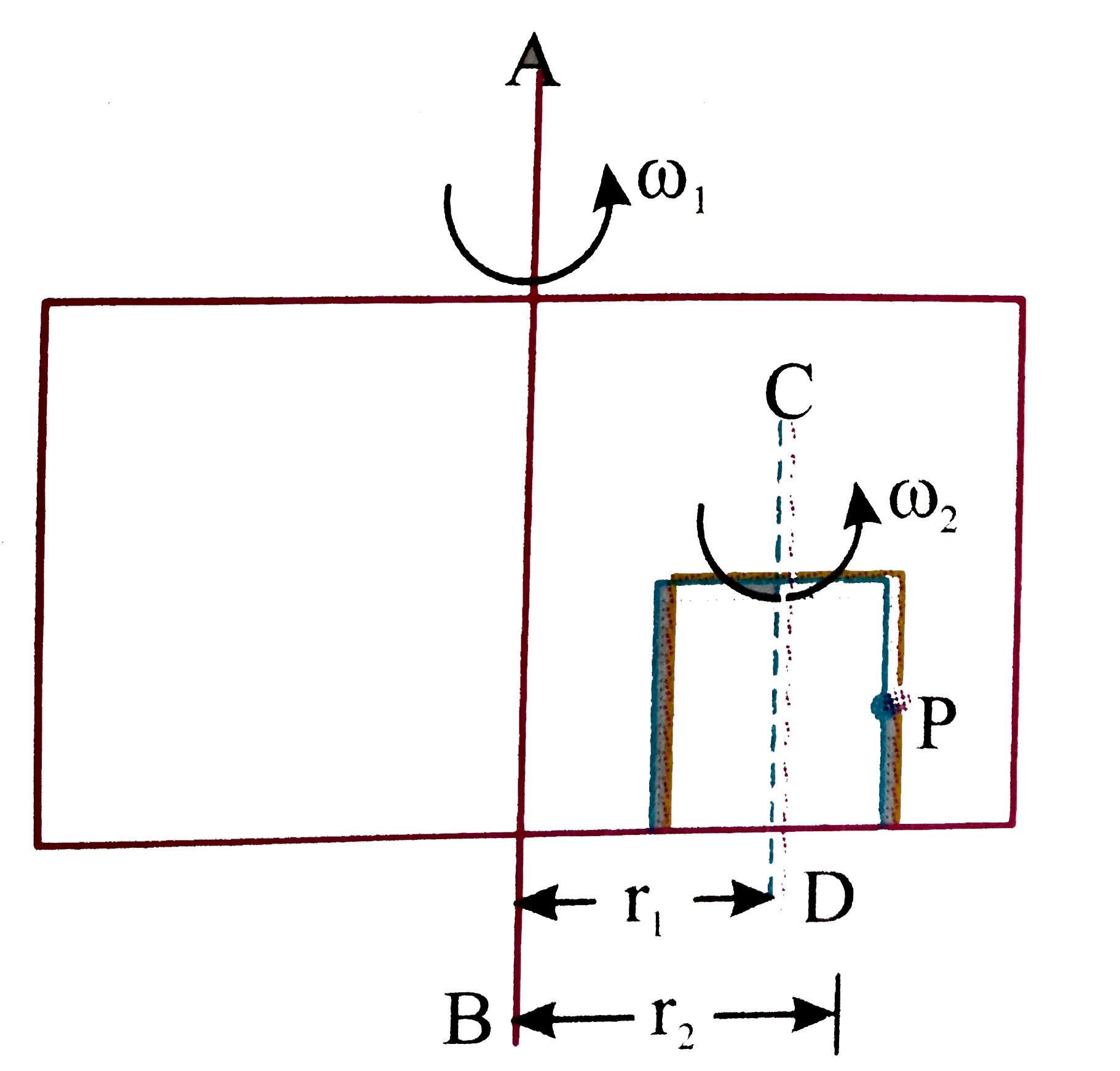 Aω2(r2−r1)+ω1r2r2Bω2(r2−r1)+ω1r1r2Cω1Dω2
Aω2(r2−r1)+ω1r2r2Bω2(r2−r1)+ω1r1r2Cω1Dω2
An earth satellite is revolving in a circular orbit of radius a withh a velocity v0. A gun in the satellite is directly aimed toward earth. A bullet is fired from the gun with muzzle velocity v02. Find the ratio of distance of farthest and closest approach of bullet from centre of earth. (Assume that mass of the satellite is very-very large with respect to the mass of the bullet)
View SolutionA ball of mass m is shot with a velocity u at an angle 0 with the horizontal which strikes the box of mass M resting at the edge of a smooth table as shown in figure . After striking the box ball falls down vertically. Find the value of u such that the box is raised to the point A shown in figure. Also find the horizontal distance l from which shot was fired.

View SolutionA container contains an incompressible and non - viscous liquid of density ρ and is filled upto a height H . Now if container is moved towards right with an acceleration a then find the horizontal force exerted by liquid on the face ABCD of container . Assume container have enough height so that liquid does not fall outside the container .

View SolutionA particle slides down on a smooth incline of inclination 30∘, fixed in an elevator going up with an acceleration 2m/s2. The box of incline has width 4m. The time taken by the particle to reach the bottom will be

View SolutionA rocket is fired and ascends with constant vertical acceleration of 10m/s2 for 1 minute. Its fuel is exhausted and it continues as a free particle. The maximum altitude reached is (g=10m/s2)
View Solution
