A ball is thrown upwards from the top of an incline with angle of projection θ with the vertical as shown. Take θ=60∘ and g=10m/s2 . The ball lands exactly at the foot of the incline.
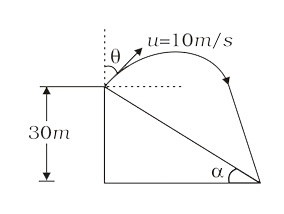
The time of flight of the ball is:
t=√3s
t = 4 s
t = 3 s
t = 6 s
The correct Answer is:C
uy=10cos60∘=5m/s⇒5t−12>2=−30⇒t2−t−6=0⇒t=3s
Similar Questions
A ball is thrown downwards with a speed of 20ms–1 from top of a building 150m high and simultaneously another ball is thrown vertically upwards with a speed of 30ms–1 from the foot of the building. Find the time after which both the balls will meet - (g=10ms–2)
View SolutionA ball is dropped from the height h on an inclined plane of inclination θ. If the coefficient of restitution is e, at what distance along the plane , the ball again collides with the plane.
View Solution
Knowledge Check
A ball is thrown upwards from the top of an incline with angle of projection θ with the vertical as shown. Take θ=60∘ and g=10m/s2 . The ball lands exactly at the foot of the incline.

The angle of inclination of incline α is:Atan−1(3)Btan−1(6)Ctan−1(√3/2)Dtan−1(2/√3)A ball is thrown vertically upwards from the top of tower of height h with velocity v . The ball strikes the ground after time.
Avg[1+√1+2ghv2]Bvg[1+√1−2ghv2]Cvg(1+2ghv2)1/2Dvg(1−2ghv2)1/2A ball is thrown upwards from the top of a tower 40m high with a velocity of 10m/s. Find the time when it strikes the ground. Take g=10m/s2.
A4sB−28sC12sD−2s
A ball is thrown upwards from the ground with an initial speed of u. The ball is at height of 80m at two times, the time interval being 6 s. Find u. Take g=10m/s2.
View SolutionA ball is thrown vertically upwards from the ground. Work done by air resistance during its time of flight is
View SolutionA ball is thrown upward with speed 10 m/s from the top to the tower reaches the ground with a speed 20 m/s. The height of the tower is [Take g=10m/s2]
View SolutionA ball is projected from the bottom of an inclined plane of inclination 30∘, with a velocity of 30ms−1, at an angle of 30∘ with the inclined plane. If g=10ms−2 , then the range of the ball on given inclined plane is
View SolutionTwo balls are thrown from an inclined plane at angle of projection α with the plane, one up the incline and other down the incline as shown in figure (T stands for total time of flight):
View Solution

