A car is traveling at a velocity of 10 km/h on a straight road. The driver of the car throws a ball. If the ball is to reach back to the driver, the direction of throw makes the following angle with the direction of the car:
135∘
90∘
tan−1√2
tan−1(1√2)
The correct Answer is:B
To solve the problem of determining the angle at which the driver must throw the ball so that it returns to him while the car is moving forward, we can follow these steps:
1. Understand the Situation:
- The car is moving at a velocity of vc=10km/h.
- The driver throws a ball with a velocity u at an angle θ with respect to the direction of the car.
2. Define the Velocities:
- The velocity of the ball with respect to the car is →u.
- The velocity of the car is →vc.
3. Components of the Ball's Velocity:
- The velocity of the ball with respect to the ground can be expressed as:
→vb=→u+→vc
- The x-component of the ball's velocity (in the direction of the car) is given by:
vbx=ucosθ+vc
- The y-component of the ball's velocity (perpendicular to the car's direction) is:
vby=usinθ
4. Condition for the Ball to Return:
- For the ball to return to the driver, it must have the same horizontal velocity as the car after being thrown. Thus, we set the x-component of the ball's velocity equal to the velocity of the car:
ucosθ+vc=vc
5. Simplifying the Equation:
- Rearranging the equation gives:
ucosθ=0
- This implies that:
cosθ=0
6. Finding the Angle:
- The angle θ for which cosθ=0 is:
θ=90∘
Conclusion:
The driver must throw the ball at an angle of 90∘ to the direction of the car for it to return to him.
- The car is moving at a velocity of vc=10km/h.
- The driver throws a ball with a velocity u at an angle θ with respect to the direction of the car.
- The velocity of the ball with respect to the car is →u.
- The velocity of the car is →vc.
- The velocity of the ball with respect to the ground can be expressed as:
→vb=→u+→vc
- The x-component of the ball's velocity (in the direction of the car) is given by:
vbx=ucosθ+vc
- The y-component of the ball's velocity (perpendicular to the car's direction) is:
vby=usinθ
- For the ball to return to the driver, it must have the same horizontal velocity as the car after being thrown. Thus, we set the x-component of the ball's velocity equal to the velocity of the car:
ucosθ+vc=vc
- Rearranging the equation gives:
ucosθ=0
- This implies that:
cosθ=0
- The angle θ for which cosθ=0 is:
θ=90∘
The driver must throw the ball at an angle of 90∘ to the direction of the car for it to return to him.
Similar Questions
A car travelling with a velocity of 50kmh−1 on a straight road is ahead of a motor-cycle travelling with a speed of 75kmh−1. How would the relative velocity be altered if motor cycle is ahead of car ?
View SolutionA car travelling with a velcity of 60kmh−1 on a straight road is ahead of a motor cycle travelling with a speed of 76kmh−1. How would the relative velcity be alterd if motor cucle is ahead of car?
View Solution
Knowledge Check
A car is travelling at a velocity 10 km h−1 on a straight road. The driver of the car throws a parcel with a velocity 10√2kmh−1 with respect to the car, when the car is passing by a man standing on the side of the road. If the parcel is to reach the man, the direction of throw makes the following angle with the direction of motion of the car
A135∘B45∘Ctan−1√2Dtan−1(1√2)A railroad car is moving in the +x direction on a straight and level track A person in the railroad car throws a ball the ball follows trajectory shown relative to the railroad car from an inspection of the trajectory what can be concluded about the motion of railroad car ? Treaty axis along vertical
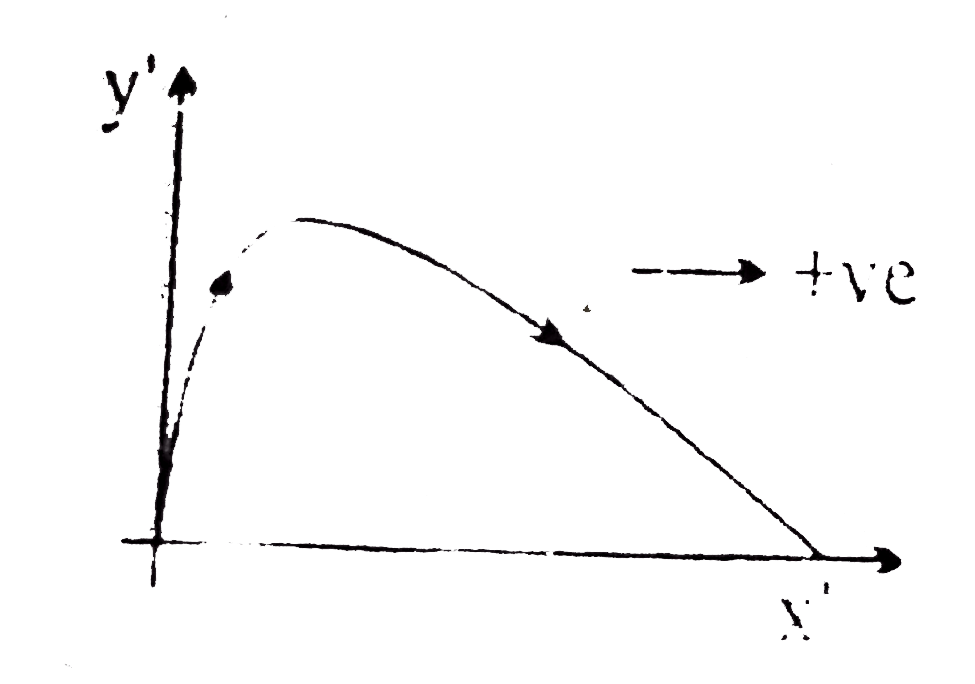 Ait is moving at a constant speedBit is speeding upCit is slowing downDnone of the above can be concluded
Ait is moving at a constant speedBit is speeding upCit is slowing downDnone of the above can be concludedA car is travelling with a speed of 36 km/hr.The driver applies the brakes & retard the car uniformly.The car is stopped in 5 seconds. The retardation of the car
A2 m/s^2B3ms2C4ms2D6ms2
A car travelling at a speed of 45 km/h takes 20 minutes to reach its destination. What distance has the car travelled?
View SolutionA car is moving at a constant speed of 40 km/h along a straight road which heads towards a large vertical wall and makes a sharp 900 turn by the side of the wall. A fly flyingat constant speed of 100 km/h, starts from the wall towrds the car t an instant when the car is 20 km away,flies until it reaches the glasspane of the car and returns to teh wll at teh same speed. It continues to fly between the car and teh wall time the car makes the 900 turn. a. What is the total distance the fly has travelled during the period?b. How many trips has it made between the car and the wall?
View SolutionA car is travelling on a straight road leading to a tower. From a point at a distance of 500 m from the tower, as seen by the driver, the angle of elevation of the top of the tower is 30∘. After driving towards the tower for 10 seconds, the angle of elevation of the top of the tower as seen by the driver is found to be 60∘. Then the speed of the car is
View SolutionWhen a car driver travelling at a speed of 10 m/s applies brakes and brings the car to rest in 20 s, then retardation will be :
View SolutionA motor car A is travelling with a velocity of 20m/s in the north-west direction and another motor car B is travelling with a velocity of 15m/s in the north-east directions.The magnitude of relative velocity of B with respect to A is.
View Solution

