What is centripetal acceleration ? Find its magniude and direction in case of a uniform circualar motion of an object .
Video Solution
Text Solution
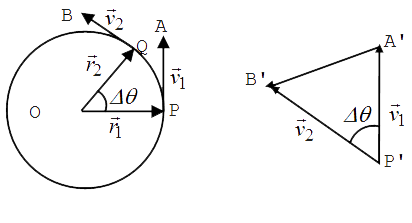
When an object moves in a circular path with constant speed, the direction of velocity changes at every point in its path, due to which an acceleration will be produced towards the centre of the circle which is called centripetal acceleration. Let, m-mass of the particle, v-constant speed, uniform angular speed, r-radius of the circular path
At any time t, the particle is at P with position vector the particle is at Q with position vector such that = omega=triangletheta//triangle t " Let, "vecv_(1) and vecv_(2)|vecPA|=|vecQB|=voverset(-)(P'A') and overset(-)(P'B')" as the velocity vectors "overset(-)v_(1) and overset(-)v_(2)overset(-)P' A'+ overset(-)A'B'=overset(-)P'B or =overset(-)(A'B') =overset(-)(P'B')- overset(-)(P'A') =overset(-)(v_(2))-overset(-)(v_(1))=trianglevecttriangle to 0 A'B'therefore triangletheta=A'B'//P'A' =|trianglev|//|vecv|, omegatrignalet=|trianglevecv|//|vecv| and |trianglevecv|//|trianglevect|= |vecv|omega=(omega r)omega=omega^(2) r [v=omegar]trianglet to 0" then " |trianglevecv|//|trianglevect||veca|=|trianglevecv|//|trianglet|=omega^(2)r=(v//r)^(2)r=v^(2)//r|veca|=omega^(2)=v^(2)//rtrianglettrianglethetaangleABC=angleACB=90^(@)trianglevecvvecavecv_(1) " But "vecv_(1)veca(=v^(2)/r) but its direction continuously changes and remains perpendicular to the velocity vector at all positions.
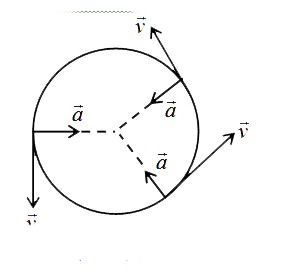
|
Similar Questions
Knowledge Check
If an object undergoes a uniform circular motion, then its
Aacceleration remains uniformBvelocity changesCspeed changesDvelcoity remains uniformIn case of uniform motion acceleration is
AZeroBPositiveCNegativeDNone of these.In case of a uniform circular motion, velocity and acceleration are
AperpendicularBin same directionCin opposite directionDnot related to each other
Non Uniform Accelerated Motion
View SolutionWhat is the magniude and direction of (ˆI+ˆj)?
View SolutionWhat is the relation between Time period and Frequency in case of uniform circular motion ?
View SolutionThe direction of centripetal acceleration or radian acceleration
View SolutionIn the following questions a statement of assertion (A) is followed by a statement of reason ( R).
A : A uniform circular motion have non uniform acceleration .
R: The direction of acceleration of a particle in uniform circular motion changes continuously .
View Solution