Area lying in the first quadrant and bounded by the circle x2+y2=4 and the lines x=0andx=2 is
(A) π (B) π2 (C) π3 (D) π4
Video Solution
Text Solution
The correct Answer is:A
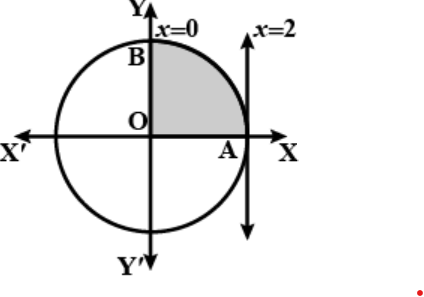
The area bounded by the circle and the lines, x=0 and x=2, in the first quadrant is represented as shaded region in the plot.
Area of △OAB=∫20ydx
=∫20√4−x2dx
=[x2√4−x2+42sin−1(x2)]20
=2(π2) = π sq. units
|
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
Area lying in the first quadrant and bounded by the circle x2+y2=4 the line x=√3y and x-axis , is
AπBπ/2Cπ/3DNone of these - Question 2 - Select One
The area lying in the first quadrant and bounded by the circle x2+y2=4 and the line x=√3y is :
Aπ3Bπ2CπDπ5 - Question 3 - Select One
Area lying in the first quadrant and bounded by the circle x2+y2=4 the line x=√3y and x-axis , is
AπBπ/2Cπ/3Dπ/4
The area of the region lying in the first quadrant and bounded by the curve y=4x2, and the lines y =2 and y =4 is "___________"
View SolutionThe angle between the planes 2x−y+z=6andx+y+2z=7 is (A) π4 (B) π6 (C) π3 (D) π2
View SolutionCircumference of the circle touching the lines 3x+4y-3=0,6x+8y-1=0 is
(A) π(B)π3(C)6π(D)π2View SolutionFind the area of the region bounded by the curve y=sinx, the lines x=−π2,x=π2 and X- axis.
View SolutionArea bounded by the curve y=sin2x and lines x=π2,x=π and X-axis is
View Solution

