निम्नलिखित परिभाषित प्रत्येक द्विआधारी संक्रिया * के लिए निर्धारित कीजिए कि क्या संक्रिया * क्रमविनिमेयी (commutative) है तथा क्या संक्रिया * साहचर्यी (associative) है ?
Q में a * b = द्वारा परिभाषित।
The correct Answer is:हाँ।
Step by step video, text & image solution for निम्नलिखित परिभाषित प्रत्येक द्विआधारी संक्रिया * के लिए निर्धारित कीजिए कि क्या संक्रिया * क्रमविनिमेयी (commutative) है तथा क्या संक्रिया * साहचर्यी (associative) है ? Q में a * b = (ab)/4 द्वारा परिभाषित। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- सम्बन्ध और फलन Book:SHIVLAAL PUBLICATIONChapter:सम्बन्ध और फलन Exercise:वस्तुनिष्ठ प्रश्न
Explore 56 Videos
- सम्बन्ध और फलन Book:SHIVLAAL PUBLICATIONChapter:सम्बन्ध और फलन Exercise:प्रश्नावली 1 (G)
Explore 12 Videos
- समाकलन के अनुप्रयोग Book:SHIVLAAL PUBLICATIONChapter:समाकलन के अनुप्रयोग Exercise:दीर्घ उत्तरीय प्रश्न
Explore 16 Videos
- सम्बन्ध एवं फलन Book:SHIVLAAL PUBLICATIONChapter:सम्बन्ध एवं फलन Exercise:दीर्घ उत्तरीय प्रश्न
Explore 35 Videos
Similar Questions
यदि R एक सममित सम्बन्ध हो, तब
View Solutionनिर्धारित कीजिए कि क्या निम्नलिखित प्रकार से परिभाषित प्रत्येक संक्रिया ' * ' संक्रिया प्राप्त होती है या नहीं :
N में, a*b = a-b से परिभाषित संक्रिया*
View Solutionरेखा xa+yb=1 तथा निर्देशाक्षो के बीच क्षेत्रफल ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए कि R में R={(a,b),a≤b} द्वारा परिभाषित सम्बन्ध स्वतुल्य तथा संक्रामक है किन्तु सममित नहीं है?
View Solutionअऋण (Non - negative ) संख्याओं के समुच्चय W पर संक्रियां * निम्न प्रकार परिभाषित है a ∗b=a^(b) सिद्ध कीजिए की * समुच्चय W पर द्विआधारी संक्रिया नहीं है|
View SolutionZ में a∗b =a-bद्वारा परिभाषित द्विआधारी संक्रिया*के लिए निर्धारित कीजिए कि क्या*द्विआधारी, क्रमविनिमेय तथा साहचर्य है ?
View Solutionएक द्विआधारी संक्रिया ∗Z+ पर निम्न रूप परिभाषित है :
a∗b=ab−bजहाँa,b∈Z+
2∗5 का मान ज्ञात कीजिए , जहाँ Z+ धनात्मक पूर्णांकों का समुच्चय है ।
View Solutionमाना कि N में एक द्वि - आधारी संकिया ∗, a∗b=a तथा b के LCM द्वारा परिभाषित है , a,b∈N तब सिद्ध कीजिए कि :(20∗16)∗8=20∗(16∗8)
View Solutionमान लीजिए कि R में द्वि -आधारी संक्रिया ∗,a∗b=1+ab,a,b∈R, तो संक्रिया ∗ :
(i) क्रम - विनिमेय है किन्तु साहचर्य नहीं है । , (ii) साहचर्य है किन्तु क्रम - विनिमेय नहीं है ।
(iii) न तो क्रम - विनिमेय है और न साहचर्य है । , (iv) क्रम - विनिमेय तथा साहचर्य दोनों ही है ।
View Solutionसिद्ध कीजिए कि ∗R×R→R,(a,b)→a+5b3 द्वारा प्रदत्त एक द्विआधारी संक्रिया है।
(यहाँ a∗b=a+5b3,a,b∈R )
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionयदि संक्रिया ∗ वास्तविक संख्याओं के समुच्चय R पर द्विआधारी संक्रिया है तथा इस प्रकार परिभाषित है कि
a∗b=√a4+b4 , जहाँ a,b∈R से दिखाइए कि '∗' क्रम-विनिमेय नियम का पालन करती है।
View Solutionयदि द्विआधारी संक्रिया ∗ वास्तविक संख्याओं के समुच्चय R पर इस प्रकार परिभाषित है कि
a∗b=ab2+1, जहाँ a,b∈R
तो द्विआधारी संक्रिया ∗ के साहचर्यता (associativity) की जाँच कीजिए।
View Solutionएक फलन g जो प्रत्येक वास्तविक संख्या x>0 के लिए परिभाषित है तथा g(1)=1,g'(x2)=x3 को सभी x>0 के लिए सन्तुष्ट करता है, तो g (4) का मान है
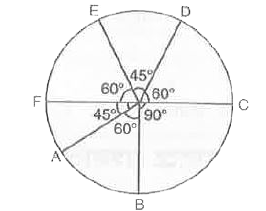
View Solutionनिम्नलिखित के उत्तर दीजिए और उनके कारण भी दीजिए :
(i ) क्या AB = BC है?
(ii ) क्या AB = DC है?
(iii ) क्या DE = AF है?
(iv ) क्या EF = AB है?
(v ) क्या BC = EF है?
(vi ) क्या AB = DC = EF है?
View Solutionलोकतंत्र को परिभाषित करने के तरीके|| शासन का सर्वाधिक प्रचलित रूप|| लोकतंत्र के विकल्प क्या है
View Solution