किसी M द्रव्यमान तथा R त्रिज्या वाले एक पहिये के किनारे (rim) पर एक रैखिक आवेश स्थापित किया गया है जिसकी प्रति इकाई लम्बाई पर आवेश का मान λ है। पहिये के स्पोक (spoke) हल्के और कुचालक है तथा वह अपनी अक्ष के परित: घर्षण रहित घूर्णन हेतु स्वतंत्र है जैसा कि चित्र में दर्शाता गया है। पहिये के वृत्तीय भाग पर रिम के अंदर एकसमान चुम्बकीय क्षेत्र विस्तरित है। इसे इस प्रकार परिभाषित किया गया है,
B=−B0k (r≤a,a≤R)
= 0 (अन्यथा)
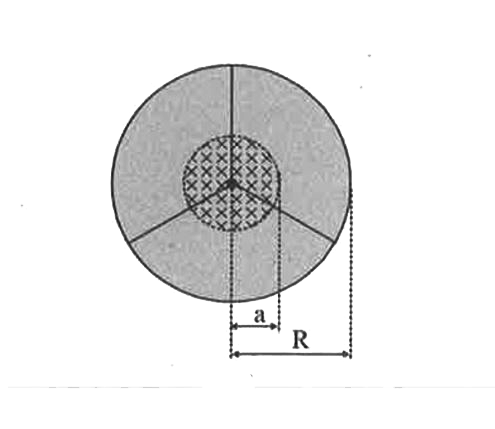
चुम्बकीय क्षेत्र को अचानक 'ऑफ़' (switched off) करने के पश्चात पहिये का कोणीय वेग ज्ञात कीजिये।
M द्रव्यमान तथा R त्रिज्या के चक्र कि कोणीय चाल माना ω है।
माना उत्पन्न प्रेरण वि. वा. बल =ε
घूर्णित चक्र की घूर्णन गतिज ऊर्जा (K.E)=12IΩ2 ...(1)
जहाँ पर I = चक्र का जड़त्व आघूर्ण है।
I=12MR2 ...(2)
किया गया कार्य
कार्य ऊर्जा सिद्धांत को लगाने पर-
घूर्णन गतिज ऊर्जा (K .E.) = किया गया कार्य
K.E=Q×ε ....(3)
हम जानते है कि एकसमान चुम्बकीय क्षेत्र में घूर्णन करती छड़ का वि. वा. बल =12Bωa2 द्वारा दिया जाता है। चूंकि यहाँ चुम्बकीय क्षेत्र परिवर्तनशील है, इस कारण से वि. वा. बल का औसत मान
12(12Bωa2)=14Bωa2 द्वारा दिया जाता है।
=14Bωa2...(4)
अब आवेश Q=λ.2πR
Q=2πRλ....(5)
अत: समीकरण 1 व 3 से Q×ε=12Iω2
सभी का मान उपरोक्त समीकरणों से रखने पर
2πRλ×14Bωa2=12MR2ω2
⇒12πRλBωa2=12MR2ω2
या ω=Bπa2λRMR2=Bπa2λMR
चुम्बकीय क्षेत्र के अनुदिश अर्थात ˆk दिशा में दिशा जोड़कर
→ω=−B0πa2λMRˆk
Topper's Solved these Questions
- विद्युत चुम्बकीय प्रेरण BOOK - SANJEEV PUBLICATIONCHAPTER - विद्युत चुम्बकीय प्रेरण EXERCISE - निबंधात्मक प्रश्न
7 Videos
- प्रत्यावर्ती धाराBOOK - SANJEEV PUBLICATIONCHAPTER - प्रत्यावर्ती धाराEXERCISE - अन्य महत्वपूर्ण प्रश्न
96 Videos
- विद्युत धारा BOOK - SANJEEV PUBLICATIONCHAPTER - विद्युत धारा EXERCISE - उच्चस्तरीय बुद्धि-कौशल प्रश्न
11 Videos
Similar Questions
विद्युत चुंबकीय प्रेरण कि परिघटना को उदाहरण देकर समझाइये तथा विद्युत चुंबकीय प्रेरण संबंधी फैराडे के नियम बताइये।
View Solutionप्रत्यावर्ती धारा के वर्ग माध्य मूल मान को परिभाषित कीजिये।
View Solutionधातु के आयन्स से दो टक्करों के मध्य मुक्त इलेक्ट्रॉन्स द्वारा तय किये गये पथ की प्रकृति क्या होती है?
View Solutionनिम्न कथन सत्य है अथवा असत्य-
उद्देश्य फलन का अधिकतम मान, परिबद्ध क्षेत्र के किसी एक शीर्ष पर होता है।
View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionकॉलम - I में कुछ निश्चित स्थितियां दी गई है जिनमे प्रतिरोध का सीधा धात्विक तार प्रयुक्त किया है तथा कॉलम - II में कुछ परिणामी प्रभाव दिए है कॉलम - I के कथनो को कॉलम - II के कथनो से सुलमित कीजिए
कॉलम - I कॉलम - II(A)एक आवेशित संधारित्र को तार के सिरों से जोड़ा गया है(p) एक नियत धारा तार में से प्रवाहित होती है(B)तार को इसकी लम्बाई के लम्बवत नियत वेग से एक समान चुम्बकीय क्षेत्र में गतिमान किया जाता है चुम्बकीय क्षेत्र गति के तल के लम्बवत है(q)उष्मीय ऊर्जा तार में उत्पन्न होती है(C)तार को नियत विधुत क्षेत्र में रखा जाता है जिसकी दिशा तार की लम्बाई के अनुदिश है(r)तार के सिरों पर एक नियत विभवान्तर उत्पन्न होता है(D)तार के सिरों पर एक नियत वि. वा. बल. की बैट्री जोड़ी जाती है(s)तार के सिरों का नियत परिमाण का आवेश उपस्थित होता है
View Solutionआवेश के विशिष्ट गुण|आवेश एक अदिश राशि है|आवेश सदैव द्रव्यमान के साथ सम्बन्ध होता है|महतवपूर्ण बिंदु|आवेश का स्थानांतरण|आवेश का क्वांटिकरण|आवेश संरक्षित है|OMR|Summary
View Solutionटोरोइड के कारण चुम्बकीय क्षेत्र | एक समान चुम्बकीय क्षेत्र में गतिमान आवेश पर बल
View Solutionवैधुत क्षेत्र क्या होता है#!#एक बिंदु आवेश के लिए वैधुत क्षेत्र का सूत्र व प्रशन
View Solution5 बार और 300K पर एक आदर्श एक्परमाणविक गैस के दो मोल के 1 बार के ब्रह्म डाब तक अनुत्क्रमणीय रूप से प्रसारित किया जाता है गैस दवरा किया गया कार्य xR (बार लीटर में ) है x का मान है
View Solutionआण्विक द्रव्यमान 390 वाले एक यौगिक को प्राप्त करने के लिए आण्विक द्रव्यमान 180 वाले एक यौगिक को CH_(3)COCl के साथ ऐसिलीकृत किया जाता है। पूर्व यौगिक के प्रति अणु पर उपस्थित ऐमीनो समूहों की संख्या है:
View Solution
