A point mass is tied to one end of a cord whose other end passes through a vertical hollow tube , caught in one hand. The point mass is being rotated in a horizontal circle ofradius 2 m with speed of 4m/sec.The cord is then pulled down so that the radius of the circle reduces to 1m . Compute the new linear and angular velocities of the point mass and compute the kinetic energies under the initial and final states.

Video Solution

Text Solution

Verified by Experts

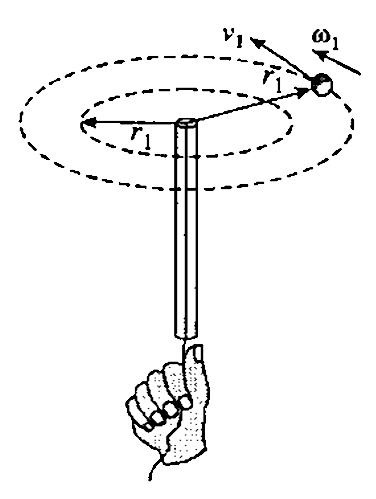
The force on the point mass due to cord is radial and hence the torque abot the centre of ratation is zero. Therefore, the angualr momentum must remain constant as the cord is shortened. Let mass of the paricel be m let it rotate initially in cricle of radius $r_{1}$ with linear velocity $v_{1}$ and angular velocity $ω_{1}$ . Furthere let the corresponding quantities in the final state be radius $r_{2}$ . linear velocity $V_{2}$ and angular velocity $ω_{2}$ .
$∴$ Initial angular momentum = Final angular momentum
$∴ I_{1} ω_{1} = I_{2} ω_{2} \Rightarrow m r_{1}^{2} \frac{v_{1}}{r_{1}} = m r_{2}^{2} \frac{v_{1}}{r_{2}} \Rightarrow r_{1} v_{1} = r_{2} v_{2}$
$∴ v_{2} = \frac{r_{1}}{r_{2}} v_{1} = \frac{2}{1} \times 4 = 8 m / s$
and $ω_{2} = \frac{v_{2}}{r_{2}} = \frac{8}{1} = 8$ rad/s.
$\frac{Final K.E}{Initial K.E} = \frac{1}{2} I_{2} ω_{2}^{2} = \frac{m r_{2}^{2} \times {[\frac{v_{2}}{r_{2}}]}^{2}}{m r_{1}^{2} \times {[\frac{v_{1}}{r_{1}}]}^{2}} = \frac{v_{2}^{2}}{v_{1}^{2}} = \frac{{(8)}^{2}}{{(4)}^{2}} = 4$ .

Updated on:21/07/2023