A uniform rod of mass m and length l can rotate freely on a smooth horizontal plane about a vertical axis hinged at point H. A point mass having same mass m coming with an initial speed u perpendicular to the rod, strikes the rod in-elastically at its free end. Find out the angular velocity of the rod just after collision?
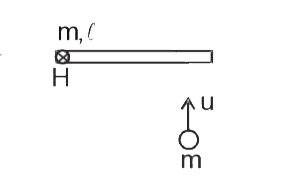
Angular momentum is conserved about H because no external force is present in horizontal plane which is producing torque about H.
μl=(ml23+ml2)ω⇒w=3u4l
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 190videos
ROTATIONAL MOTION
- BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 240videos
ROTATIONAL MOTION
- BOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-438videos
RAY OPTICS
- BOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 334videos
SEMI CONDUCTOR AND LOGIC GATES
Similar Questions
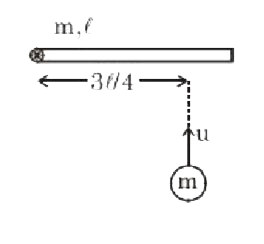
A uniform rod of mass m and length l can rotate freely on a smooth horizontal plane about a vertical axis hinged at point H. A point mass having same mass m coming with an initial speed u perpendicular to the rod, strikes the rod and sticks to it at a distance of 3l4 from hinge point. Theangular velocity of the rod just after collision is 36unl. Find the value of n.
 View Solution
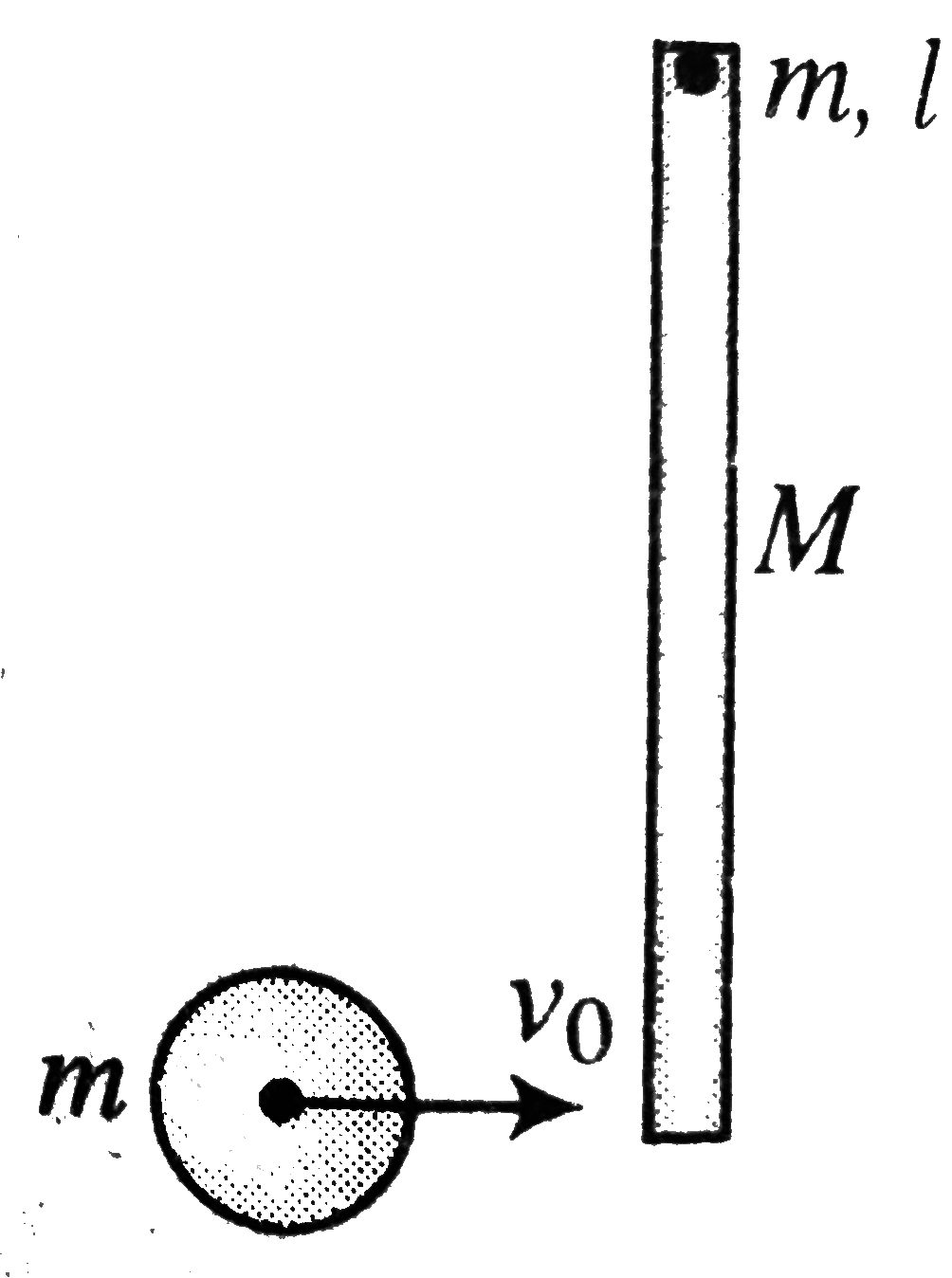
View SolutionA uniform rod of mass M and length l is placed on a smooth- horizontal surface with its one end pivoted to the surface. A small ball of mass m moving along the surface with a velocity v0, perpendicular to the rod, collides elastically with the free end of the rod. Find:
a. the angular velocity of the rod after collision.
b. the impulse applied by the pivot on the rod during collision. (Take M/m=2)
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]
A rod of mass 12 m and length l lying on a smooth horizontal plane can rotate freely about a stationary, vertical axis passing through the rod's end. A particle of mass m moving along the plane with speed v0 hits the rod's end perpendicularly and gets stuck there. Find the angular velocity of the system.
 View Solution
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA uniform rod of mass m and length l is hinged about one of its end. The hinge is smooth and rod lies on a smooth horizontal surface as shown in Fig. A particle of mass m is coming towards the rod at speed v0 perpendicular to the length of rod.
(a) Find angular velocity of the rod just after impact.

(b) Also find impulse due to hinge on rod during collision.View SolutionA uniform rod of mass m and length l can rotate in a vertical plane abota smooth horizontal axis hinged at point H. Find the force exerted by the hinge just after rod is released from rest, from initial horizontal position?
 View Solution
View SolutionA uniform rod of mass M and length L lies on a frictionless horizontal plane. A particle of same mass M moving with speed v0 perpendicular to the length of the rod strikes the end of the rod and sticks to it. Find the velocity of the center of mass and the angular velocity about the center of mass of (rod + particle) system.
View SolutionA uniform rod of mass M and length L lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance L/6 from the center and stops after the collision. Find
(a) the velocity of center of mass of rod and
(b) the angular velocity of the rod about its center just after collision.View SolutionA uniform rod AB of mass 3m and length 2l is lying at rest on a smooth horizontal table with a smooth vertical axis through the end A. A particle of mass 2m moves with speed 2u across the table and strikes the rod at its mid-point C if the impact is perfectly elastic. Find the speed of the particle after impact if
(a). It strikes rod normally,
(b). Its path before impact was inclinded at 60∘ to AC.View Solution

