Two rods each having length l and mass m joined together at point B as shown in figure.Then findout moment of inertia about axis passing thorugh A and perpendicular to the plane of page as shown in figure.
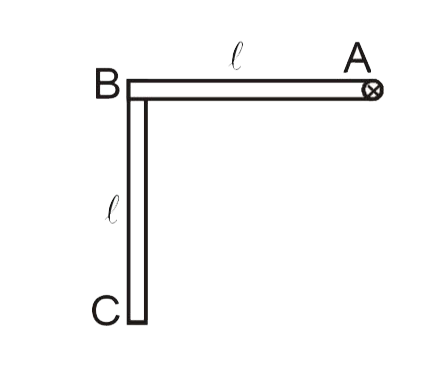
We find the resultant moment of inertia I by dividing in two parts such as
I = M.I or rod AB about A +
M.I of rod BC about A
I=I1+I2 …(1)
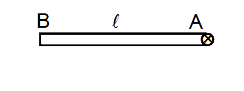
I2=ICM+md2
=ml212+5l24m ...(3)
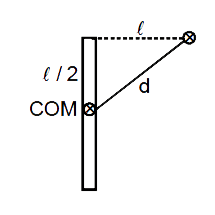
Put value from eq (2) & (3) into (1)
⇒I=ml23+ml212+ml2m4
I=ml212(4+1+15)⇒ I=5ml23
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 1
90 Videos
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 2
40 Videos
- RAY OPTICSBOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-4
38 Videos
- SEMI CONDUCTOR AND LOGIC GATESBOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 3
34 Videos
Similar Questions
For the structure shown in figure, moment of inertia about an axis passing through yy' is
_PHY_213_Q01.png)
View SolutionTwo identical rods each of mass M and length L are kept according to figure. Find the moment of inertia of rods about an axis passing through O and perpendicular to the plane of rods.
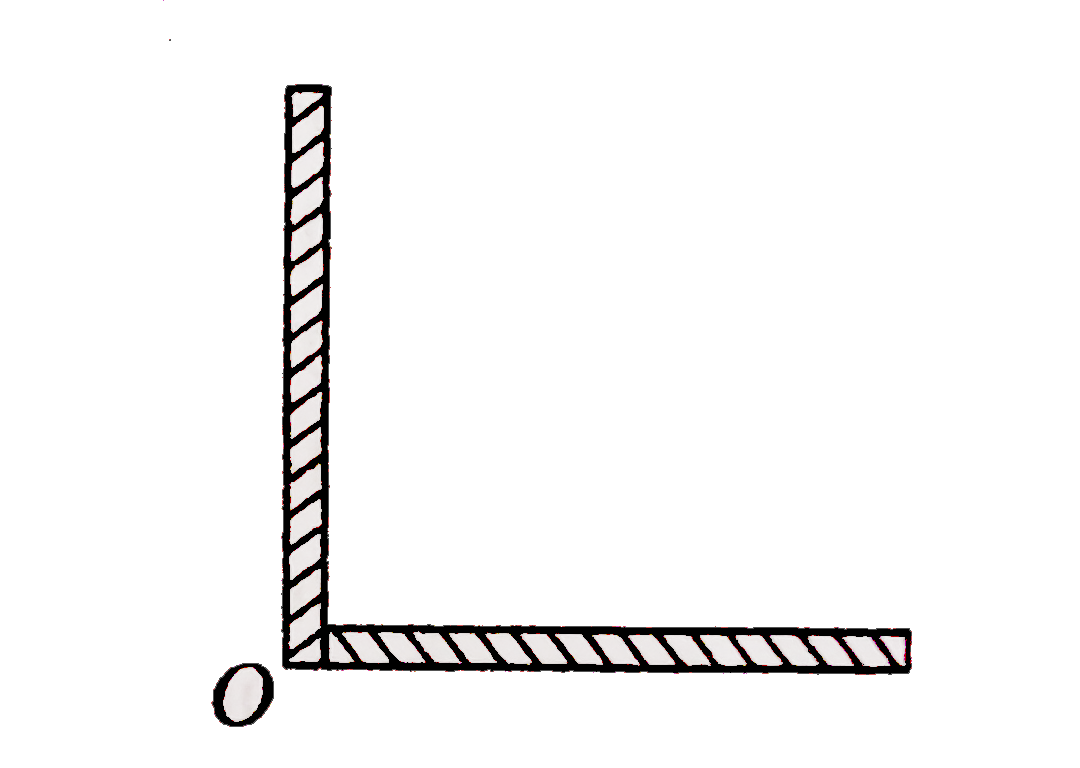
View Solution
Knowledge Check

A thin rod of length 4l, mass 4 m is bent at the point as shown in the figure. What is the moment of inertia of the rod about the axis passing through O and perpendicular to the plane of the paper?AMl23B10Ml23CMl212DMl224
A thin rod of length 4l, mass 4 m is bent at the point as shown in the figure. What is the moment of inertia of the rod about the axis passing through O and perpendicular to the plane of the paper?Aml23B10ml23Cml212Dml224A thin rod of length l and mass m is turned at mid-point O at angle of 60°. The moment of inertia of the rod about an axis passing through O and perpendicular to the plane of the rod will be
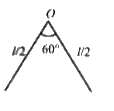 Aml2/3Bml26Cml28Dml212
Aml2/3Bml26Cml28Dml212

Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passig through its centre of mass and perpendicular to the plane of the particle.
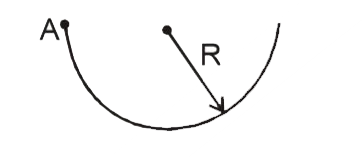
View SolutionA uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is
View SolutionA thin rod of length L of mass M is bent at the middle point O at an angle of 60∘. The moment of inertia of the rod about an axis passing through O and perpendicular to the plane of the rod will be
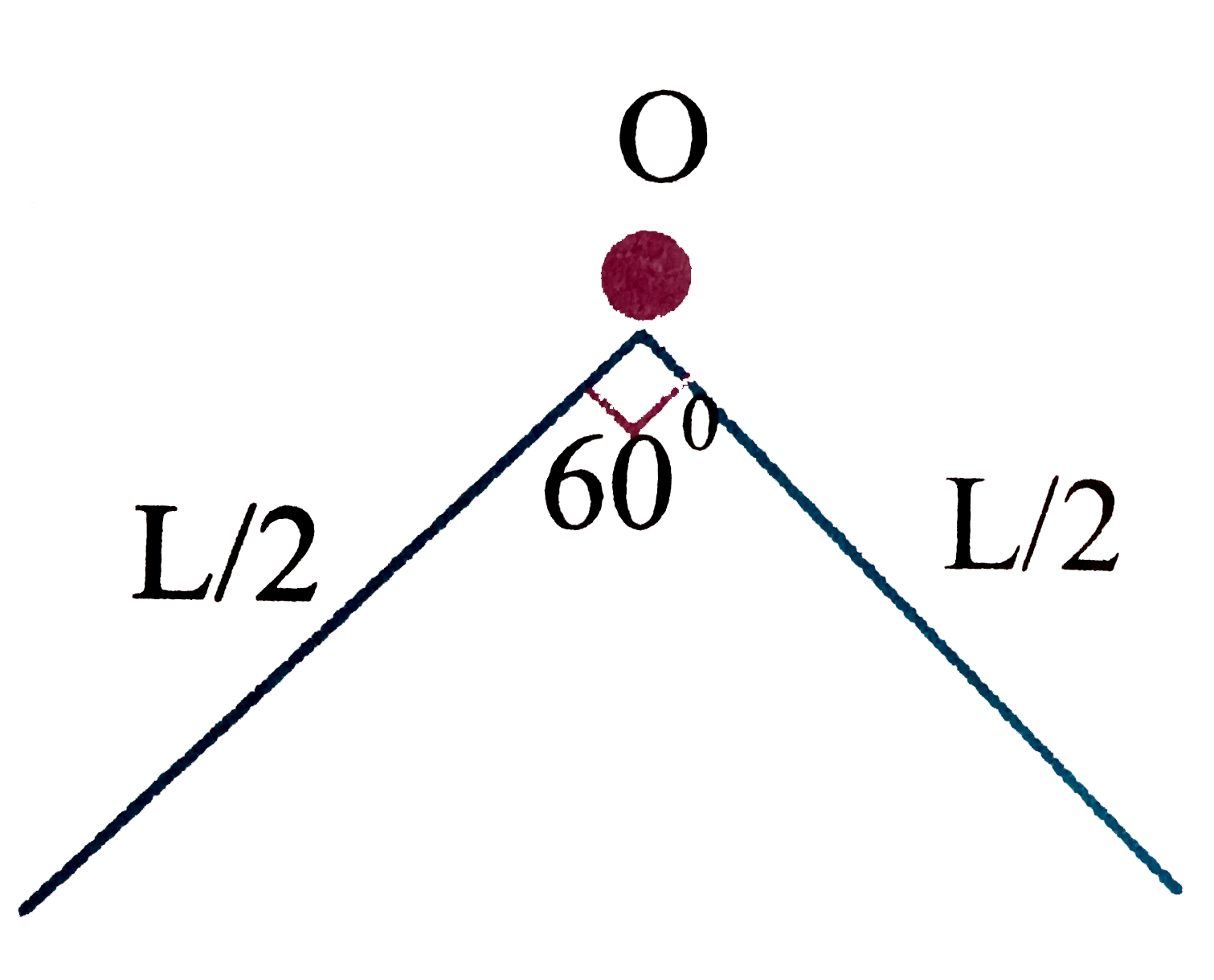
View SolutionA thin rod of length L of mass M is bent at the middle point O at an angle of 60∘. The moment of inertia of the rod about an axis passing through O and perpendicular to the plane of the rod will be

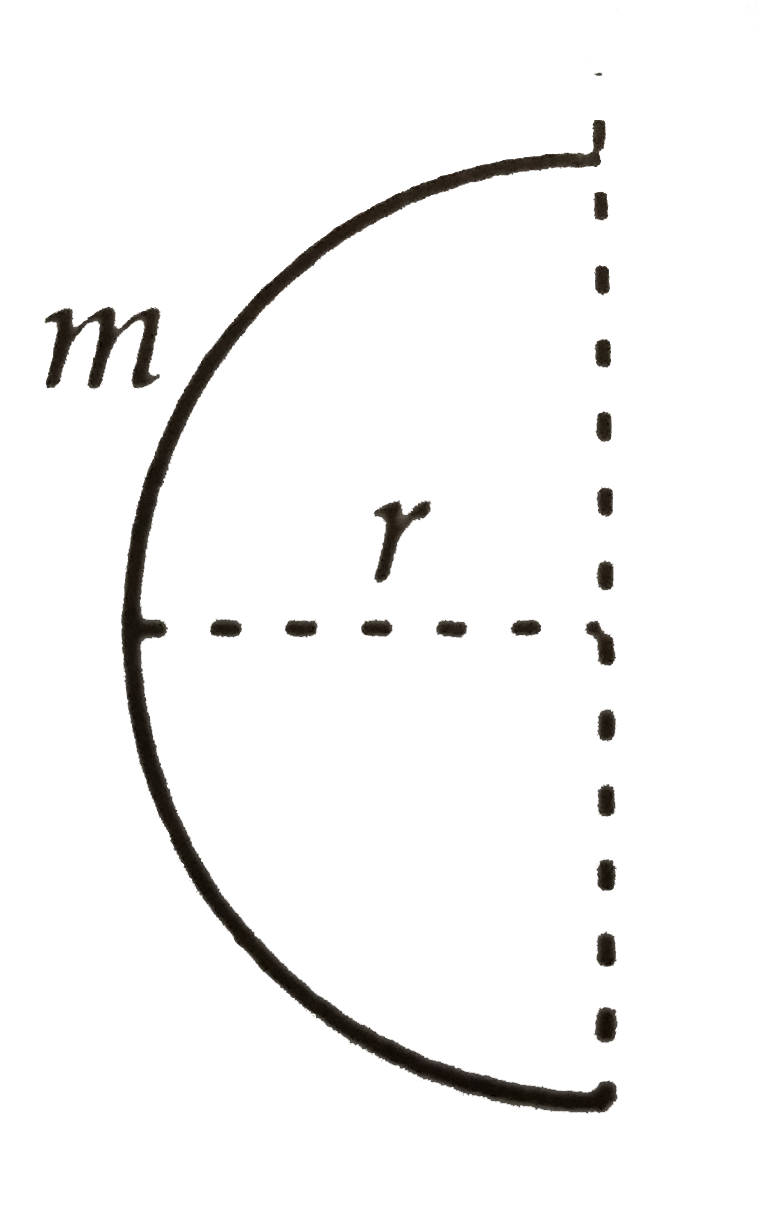
View SolutionA thin wire of length l and mass m is bent in the form of a semicircle as shown in the figure. Its moment of inertia about an axis joining its free ends will be
View Solution
