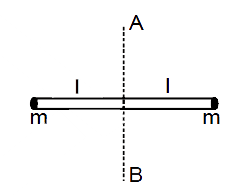
Consider a uniform rod of mass m and length 2l with two particles of mass m each at its ends. Let AB be a line perpendicular to the length of rod and passig through its centre. Find the moment of inertial of the system about AB.
IAB=Irod+Iboth particles
=m(2l)212+2(ml2)
=73ml2
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 1
90 Videos
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 2
40 Videos
- RAY OPTICSBOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-4
38 Videos
- SEMI CONDUCTOR AND LOGIC GATESBOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 3
34 Videos
Similar Questions
Consider a ligh rod with two heavy mass prticles at its ends. Let AB be as line perpendicular to the rod s shown in figure. What is the moment of inertya of the system about AB?

View SolutionConsider a uniform rod of mas M and length L. It is bent into a semicircle. Its moment of inertia about a line perpendicular to the plane wire passing through the centre is
View Solution
Knowledge Check
Moment of inertia of a thin rod of mass 'M' and length 'L' about the axis perpendicular to the rod and passing through its centre is ............
AML24BML26CML212DML22If l1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and l2 is the moment of inertia (about central axis) of the ring formed by bending the rod, then the ratio of I1 to I2 is
Al:l=1:1Bl:l=π:3Cl:l=π:4Dl:l=3:5The M.I. of thin uniform rod of mass 'M' and length 'l' about an axis passing through its centre and perpendicular to its length is
AMl2BMl2/3CMl2/2DMl2/12
find the radius of gyration of a rod of mass m and length 2l about an axis passing through one of its eneds and perpendicular to its length.
View SolutionThe moment of inertia of a straight thin rod of mass M and length l about an axis perpendicular to its length and passing through its one end, is
View SolutionCalculate the radius of gyration of a cylindrical rod of mass M and length L about an axis of rotation perpendicular to its length and passing through its centre.
View SolutionMass of thin long metal rod is 2kg and its moment of inertia about an axis perpendicular to the length of rod and passing through its one end is 0.5kgm2. Its radius of gyration is
View SolutionThe moment of inertia of a thin uniform rod of mass M and length l about an axis perpendicular to the rod through its centre is I. The moment of inertia of the rod through its end point is
View Solution
