Three known forces →Fm,→F and 2→F acting on a particle along x-axis, 120∘ with + ve x-axis and 240∘ with the + ve x-axis, respectively. The particle is moving along 60∘ with +ve x-axis. Choose correct options.
There must be a fourth force acting on the particle
There may be a fourth force acting on the particle
There must be only given three forces acting on the particle
There may be only three given forces acting on the particle
The correct Answer is:bd
To solve the problem, we need to analyze the forces acting on the particle and their resultant. Let's break it down step by step.
Step 1: Identify the Forces
We have three forces acting on a particle:
1. Force →F1 at an angle of 120∘ with the positive x-axis.
2. Force →F2 at an angle of 240∘ with the positive x-axis.
3. Force →F3=2→F which is also acting along the x-axis.
Step 2: Resolve the Forces into Components
We will resolve each force into its x and y components.
- For →F1:
F1x=F1cos(120∘)=F1(−12)=−F12
F1y=F1sin(120∘)=F1(√32)=F1√32
- For →F2:
F2x=F2cos(240∘)=F2(−12)=−F22
F2y=F2sin(240∘)=F2(−√32)=−F2√32
- For →F3=2→F:
F3x=2F(actingalongthex−axis)
F3y=0
Step 3: Calculate the Resultant Force Components
Now, we can find the resultant force components Rx and Ry:
Rx=F1x+F2x+F3x=−F12−F22+2F
Ry=F1y+F2y+F3y=F1√32−F2√32+0
Step 4: Analyze the Motion of the Particle
The particle is moving at an angle of 60∘ with the positive x-axis. This implies that the direction of the resultant force R must also be at 60∘.
The tangent of the angle gives us the relationship between the y and x components of the resultant force:
tan(60∘)=√3=RyRx
Step 5: Set Up the Equation
Substituting the expressions for Rx and Ry:
√3=F1√32−F2√32−F12−F22+2F
Step 6: Analyze the Options
1. There must be a fourth force: This is incorrect because the motion can be satisfied by the three forces.
2. There may be a fourth force: This is correct because a fourth force could exist that aligns with the resultant.
3. There must be only three forces: This is incorrect as we have established that a fourth force could exist.
4. There may be three forces: This is correct since the motion can be sustained with just the three forces.
Conclusion
The correct options are:
- Option B: There may be a fourth force.
- Option D: There may be three forces.
We have three forces acting on a particle:
1. Force →F1 at an angle of 120∘ with the positive x-axis.
2. Force →F2 at an angle of 240∘ with the positive x-axis.
3. Force →F3=2→F which is also acting along the x-axis.
We will resolve each force into its x and y components.
F1x=F1cos(120∘)=F1(−12)=−F12
F1y=F1sin(120∘)=F1(√32)=F1√32
F2x=F2cos(240∘)=F2(−12)=−F22
F2y=F2sin(240∘)=F2(−√32)=−F2√32
F3x=2F(actingalongthex−axis)
F3y=0
Now, we can find the resultant force components Rx and Ry:
Ry=F1y+F2y+F3y=F1√32−F2√32+0
The particle is moving at an angle of 60∘ with the positive x-axis. This implies that the direction of the resultant force R must also be at 60∘.
tan(60∘)=√3=RyRx
Substituting the expressions for Rx and Ry:
√3=F1√32−F2√32−F12−F22+2F
1. There must be a fourth force: This is incorrect because the motion can be satisfied by the three forces.
2. There may be a fourth force: This is correct because a fourth force could exist that aligns with the resultant.
3. There must be only three forces: This is incorrect as we have established that a fourth force could exist.
4. There may be three forces: This is correct since the motion can be sustained with just the three forces.
The correct options are:
- Option B: There may be a fourth force.
- Option D: There may be three forces.
Similar Questions
Knowledge Check
For a particle moving along the x-axis, mark the correct statement(s).
Aif x is positive and is increasing with the time, then average velocity of the particle is positive.Bif x is negative and becoming positive after some time, then the velocity of the particle is always positive.CIf x is negative and becoming less negative as time passes, then the average velocity of the particle is positive.DIf x is positive and is increasing with time, then the velocity of the particle is always positive.Two forces f1=4N and f2=3N are acting on a particle along positve X−axis and negative y−axis respectively. The resultant force on the particle will be−
A3ˆi+4ˆjB4ˆi+3ˆjC4ˆi−3ˆjD3ˆi−4ˆjA particle executes S.H.M. along x-axis. The force acting on it is given by :
AA cos (kx)BAe−kxCAkxD−Akx
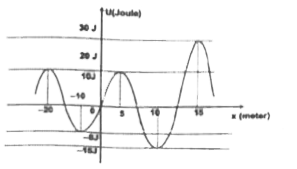
The variation of potential energy of a particle of mass m = 5kg to its x-coordinate . The particle moves under the effect of this conservative force only along the x-axis. Then, choose the correct option.
View SolutionThe X and Y components of a force F acting at 30∘ to x-axis are respectively :
View SolutionA particle moves along the X-axis as x=u(t−2s)=at(t−2)2.
View Solution.10872X2α−−→β−−→γ−−→.AZX'. Z and A are
View SolutionA particle moved along the X−axis according to the graph shown in Figure. Choose the incorrct options.

View Solution