The tension in the string is:
29.4 N
39.2 N
58.8 N
88.2 N
The correct Answer is:d
To find the tension in the string in the given arrangement, we can follow these steps:
Step 1: Understand the Forces Acting on the Object
In the given scenario, we have an object of mass m hanging from a string. The forces acting on the object include:
- The gravitational force mg acting downward.
- The tension T in the string acting upward.
- The normal force N acting perpendicular to the surface.
- The frictional force f acting opposite to the direction of motion.
Step 2: Break Down the Gravitational Force
The gravitational force can be broken down into two components:
- The component parallel to the surface: mgsinθ
- The component perpendicular to the surface: mgcosθ
Given that θ=37∘, we can calculate:
- sin37∘=0.6 (approximately)
- cos37∘=0.8 (approximately)
Thus, we have:
- mgsin37∘=0.6mg
- mgcos37∘=0.8mg
Step 3: Apply Newton's Second Law
For vertical equilibrium, the sum of the forces in the vertical direction must equal zero:
T−mgsin37∘−f=0
Where f is the frictional force, which can be expressed as:
f=μN
where μ=0.8 is the coefficient of friction.
Step 4: Calculate the Normal Force
The normal force N can be expressed in terms of the gravitational force:
N=mgcos37∘=0.8mg
Step 5: Substitute the Normal Force into the Frictional Force Equation
Now substitute N into the equation for friction:
f=μN=0.8×0.8mg=0.64mg
Step 6: Substitute Back into the Force Equation
Now substitute f back into the equilibrium equation:
T−mgsin37∘−0.64mg=0
Substituting the value of mgsin37∘:
T−0.6mg−0.64mg=0
T=0.6mg+0.64mg=1.24mg
Step 7: Calculate the Tension
Assuming g=10m/s2 and m=1kg (for simplicity):
T=1.24×10N=12.4N
Thus, the tension in the string is 12.4N.
---
In the given scenario, we have an object of mass m hanging from a string. The forces acting on the object include:
- The gravitational force mg acting downward.
- The tension T in the string acting upward.
- The normal force N acting perpendicular to the surface.
- The frictional force f acting opposite to the direction of motion.
The gravitational force can be broken down into two components:
- The component parallel to the surface: mgsinθ
- The component perpendicular to the surface: mgcosθ
- sin37∘=0.6 (approximately)
- cos37∘=0.8 (approximately)
- mgsin37∘=0.6mg
- mgcos37∘=0.8mg
For vertical equilibrium, the sum of the forces in the vertical direction must equal zero:
T−mgsin37∘−f=0
Where f is the frictional force, which can be expressed as:
f=μN
where μ=0.8 is the coefficient of friction.
The normal force N can be expressed in terms of the gravitational force:
N=mgcos37∘=0.8mg
Now substitute N into the equation for friction:
f=μN=0.8×0.8mg=0.64mg
Now substitute f back into the equilibrium equation:
T−mgsin37∘−0.64mg=0
Substituting the value of mgsin37∘:
T−0.6mg−0.64mg=0
T=0.6mg+0.64mg=1.24mg
Assuming g=10m/s2 and m=1kg (for simplicity):
T=1.24×10N=12.4N
Similar Questions
The string of a pendulum is horizontal. The mass of the bob is m. Now the string is released. The tension in the string in the lowest position is -
View SolutionIn Melde's experiment, when tension in the string is 10 g wt. then three loops are obtained. Determine the tension in the string required to obtain four leeps, if all other conditions are constant.
View Solution
Knowledge Check
A stone is tied to one end of a steing and rotated in horizontal circle with a uniform angular velocity. The tension in the string is T, if the lrngth of the string is halved and its angular velocity is doubled , the tension in the string will be
A4 TBT/2CT/4D2 TThe tension in the string in the pulley system shown in
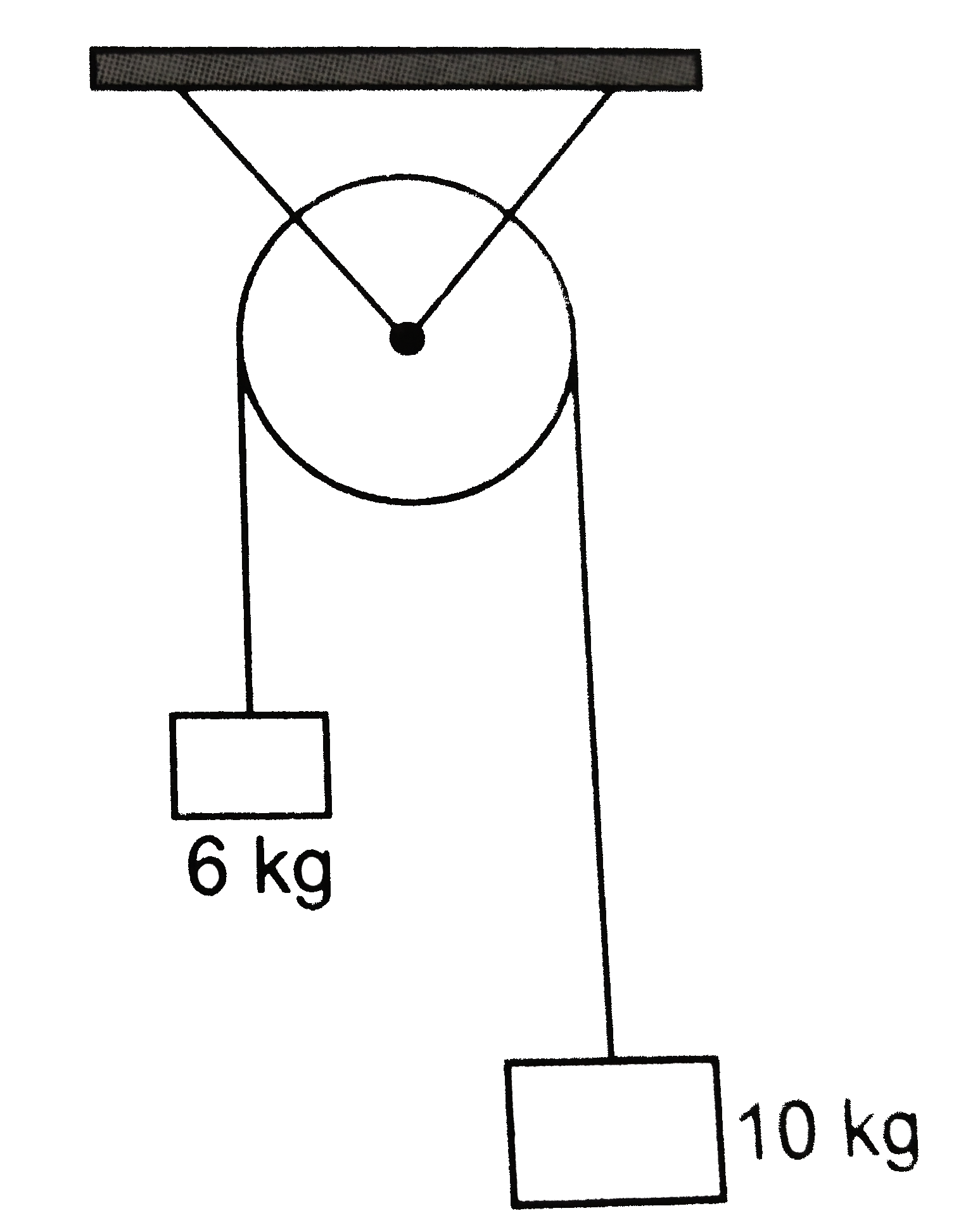 .A5.7NB7NC7.5ND73.5N
.A5.7NB7NC7.5ND73.5NA pendulum bob is hanging from the roof of an elevator with the help of a light string. When the elevator moves up with uniform acceleration 'a' the tension in the string is T1.When the elevator moves down with the same acceleration, the tension in the string is T1 .If the elevator were stationary, the tension in the string would be
AT1+T22B√T1+T2CT1T2T1+T2D2T1T3T1+T2
A pendulum bob is hanging from the roof of an elevator with the help of a light string. When the elevator moves up with uniform acceleration 'a' the tension in the string is T1. When the elevator moves down with the same acceleration, the tension in the string is T2. If the elevator were stationary, the tension in the string would be
View SolutionIn melde's experiment, the number of loops on the string changes from 5 to 4 , when the tension ine the string is increased by 0.018gm wt , then the initial tension in the string will be
View SolutionA 100 kg block is suspended with the help of three strings A, B and C. The tension in the string A is

View SolutionA sphere of radius 25 cm and mass 1 kg is hung by a string of negligible mass and length 40 cm, then tension in the string is -
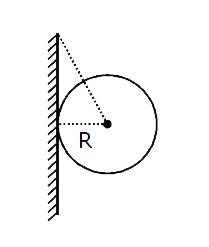
View SolutionA system is at rest as shown in figure. The tension in the string in T1. When the 2 kg block is removed, the system moves with some acceleration a and tension in string becomes T2 Find T1/T2 .
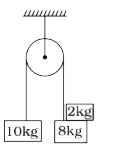
View Solution