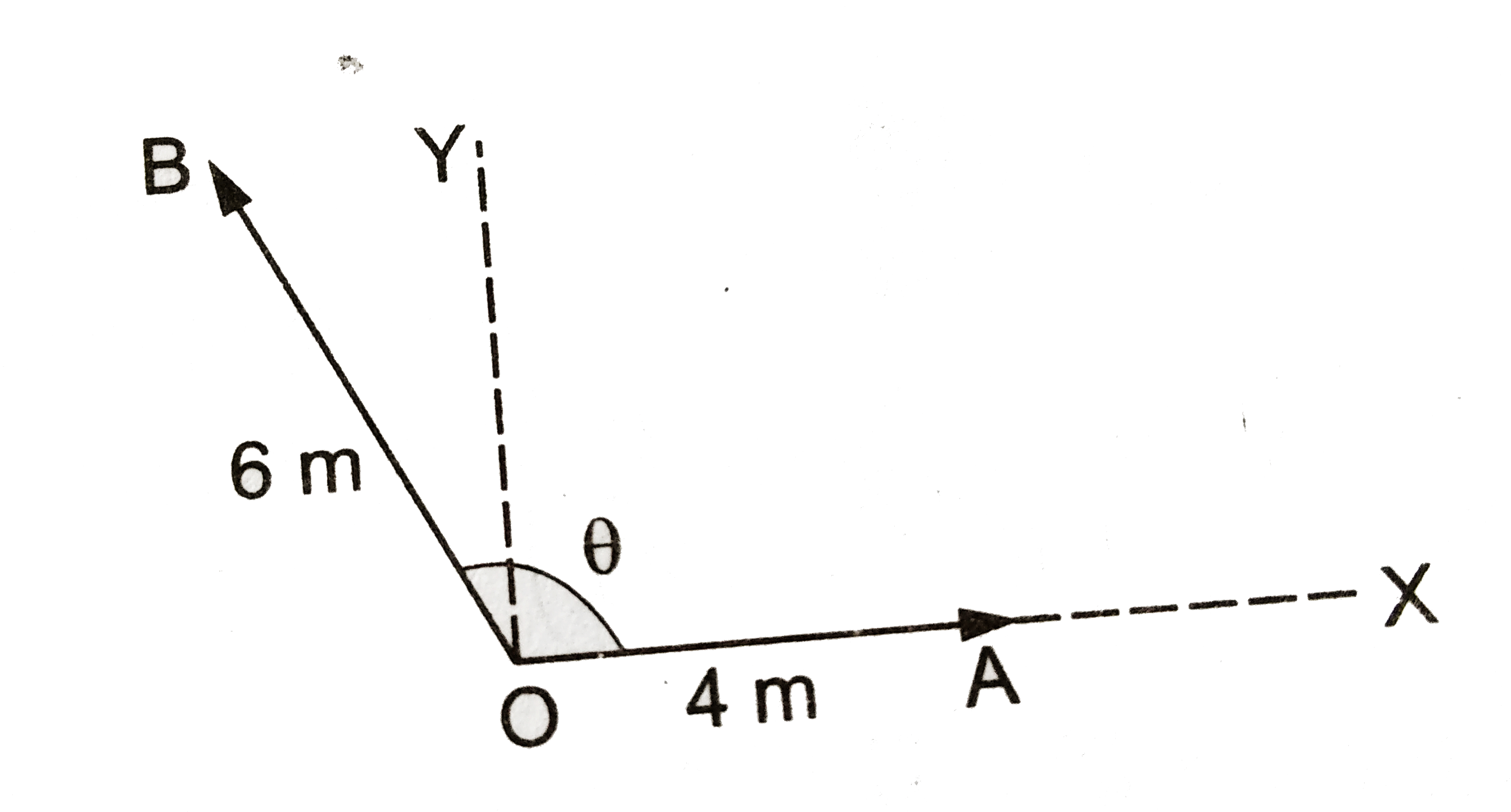
Find the resultant of the three vectors −−→OA,−−→OB and −−→OC shown in figure. Radius of the circle is R.

2R
R(1+√2)
R√2
R(√2−1)
The correct Answer is:b
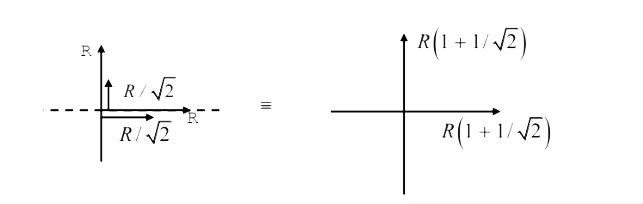
→ magnitude of resultant is
⎷R2(1+1√22)+R2(1+1√22)=R(1+√2)
Similar Questions
Knowledge Check
The resultant of the three vectors −−→OA,−−→OB and −−→OC shown in figure is
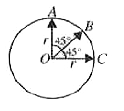 ArB2rCr(1+√s)Dr(√2−1)
ArB2rCr(1+√s)Dr(√2−1)What is the angle between the vector →A and →B as shown in figure ?
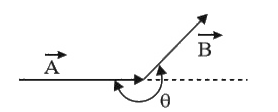 AθBπ−θCθ−πD2π−θ
AθBπ−θCθ−πD2π−θThe resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is
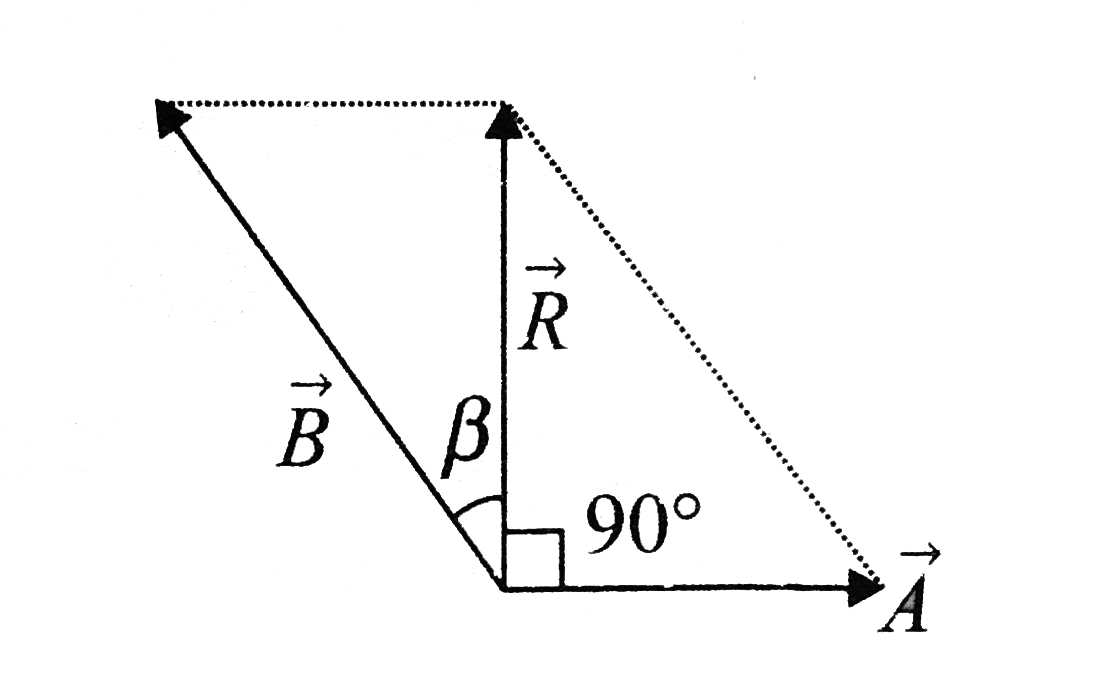 A120∘B150∘C135∘DNone of these
A120∘B150∘C135∘DNone of these
The magnitude of vectors −−→OA,−−→OBand−−→OC in figure are equal. Find the direction of −−→OA+−−→OB−−−→OC.
 .
.
View SolutionThe resultant of two velocity vectors →A and →B is perpendicular to →A. Magnitude of Resultant →R is equal to half magnitude of →B. If the angle between →A and →B is (30θ)∘, then value of θ is ?
View SolutionThe magnitudes of vectors −−→OA,−−→OB and −−→OC in figure(2-W3) are equal. Find the direction of −−→OA+−−→OB−−−→OC.
View SolutionThe sum of the three vectors shown in figure is zero. Find the magnitudes of the vectors −−→OBand−−→OC.
View SolutionABCD is a quadrilateral and E is the point of intersection of the lines joining the middle points of opposite side. Show that the resultant of −−→OA , −−→OB , −−→OC and −−→OD = 4 −−→OE , where O is any point.
View Solution