Question

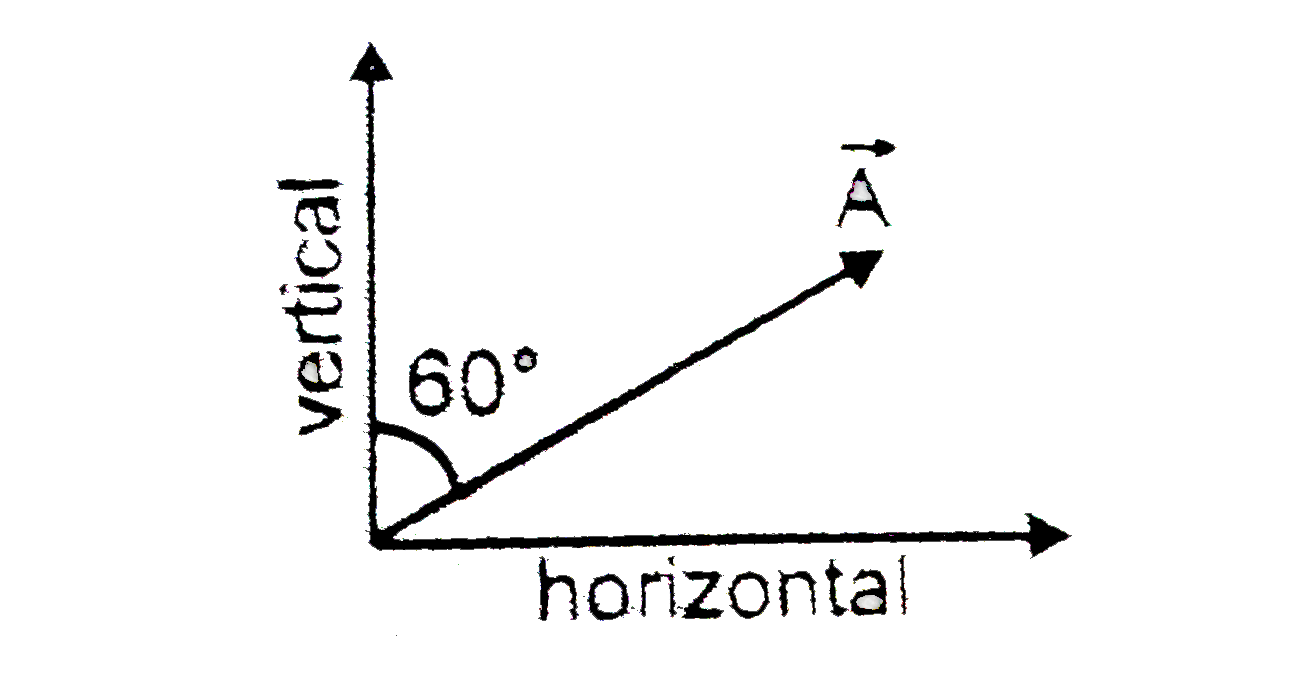
A force of 20 N is inclined to the x-axis at an angle of ${60}^{\circ }$. Calculate its x and y components.

Explanation

To find the x and y components of a force of 20 N inclined at an angle of 60° to the x-axis, we can use trigonometric functions. Here’s the step-by-step solution:

Step 1: Identify the Force and Angle
We have a force \( F = 20 \, \text{N} \) and it is inclined at an angle \( \theta = 60^\circ \) to the x-axis.

Step 2: Calculate the x-component
The x-component of the force can be calculated using the cosine function:
\( F_x = F \cdot \cos(\theta) \)
Substituting the known values:
\( F_x = 20 \cdot \cos(60^\circ) \)
We know that \( \cos(60^\circ) = \frac{1}{2} \):
\( F_x = 20 \cdot \frac{1}{2} = 10 \, \text{N} \)

Step 3: Calculate the y-component
The y-component of the force can be calculated using the sine function:
\( F_y = F \cdot \sin(\theta) \)
Substituting the known values:
\( F_y = 20 \cdot \sin(60^\circ) \)
We know that \( \sin(60^\circ) = \frac{\sqrt{3}}{2} \):
\( F_y = 20 \cdot \frac{\sqrt{3}}{2} = 10\sqrt{3} \, \text{N} \)

Step 4: Write the Final Components
Thus, the x and y components of the force are:
\( F_x = 10 \, \text{N} \, \hat{i} \)
\( F_y = 10\sqrt{3} \, \text{N} \, \hat{j} \)

Final Answer:
- The x-component of the force is \( 10 \, \text{N} \, \hat{i} \).
- The y-component of the force is \( 10\sqrt{3} \, \text{N} \, \hat{j} \).

---