What are co-initial and collinear vectors?
Step-by-Step Solution
Step 1: Define Co-initial Vectors
Co-initial vectors are vectors that originate from the same initial point. In other words, if two or more vectors start from the same point in space, they are termed co-initial vectors.
Example:
Consider two vectors OA and OB. If both vectors start from point O, then they are co-initial vectors.
Step 2: Define Collinear Vectors
Collinear vectors are vectors that lie along the same line or are parallel to each other. They can have different magnitudes and directions, but they must be aligned in such a way that they can be represented along a single straight line.
Example:
If you have two vectors that are drawn along the same line, regardless of their lengths or directions, they are considered collinear vectors.
Step 3: Summarize the Differences
- Co-initial vectors share the same starting point.
- Collinear vectors are aligned along the same line or are parallel.
Co-initial vectors are vectors that originate from the same initial point. In other words, if two or more vectors start from the same point in space, they are termed co-initial vectors.
Consider two vectors OA and OB. If both vectors start from point O, then they are co-initial vectors.
Collinear vectors are vectors that lie along the same line or are parallel to each other. They can have different magnitudes and directions, but they must be aligned in such a way that they can be represented along a single straight line.
If you have two vectors that are drawn along the same line, regardless of their lengths or directions, they are considered collinear vectors.
- Co-initial vectors share the same starting point.
- Collinear vectors are aligned along the same line or are parallel.
Similar Questions
Knowledge Check
If a and b are two non-zero and non-collinear vectors then a+b and a-b are
Alinearly dependent vectorsBlinearly independent vectorsClinearly dependent annd independent vectorsDnone of theseIf ¯a and ¯b are non-collinear vectors, then
Aonly ¯a=¯0Bonly ¯b=¯0Cboth ¯a≠¯0 and ¯b≠¯0Dboth ¯a=¯b=¯0A vector coplanar with the non-collinear vectors ¯aand¯b is
A¯aׯbB¯a+¯bC¯a.¯bD¯a×3¯b
Answer the following as true or flase: →a and →b are collinear. Two collinear vectors are always equal in magnitude. Zero vector is unique. Two vectors having same magnitude are collinear. Two collinear vectors having the same magnitude are equal.
View SolutionExplain (i) Unit vector (ii) Equal vectors (iii) Negative vectors, (iv) Coinitial v ectors (v) Collinear vectors and (vi) Copanar vectors.
View SolutionAnswer the following as true or false.
Two collinear vectors are always equal in magnitude.
View SolutionIn the following figure, which of the vectors are:
(i) Collinear
(ii) Equal
(iii) Co-initial
(iv) collinear but not equal .
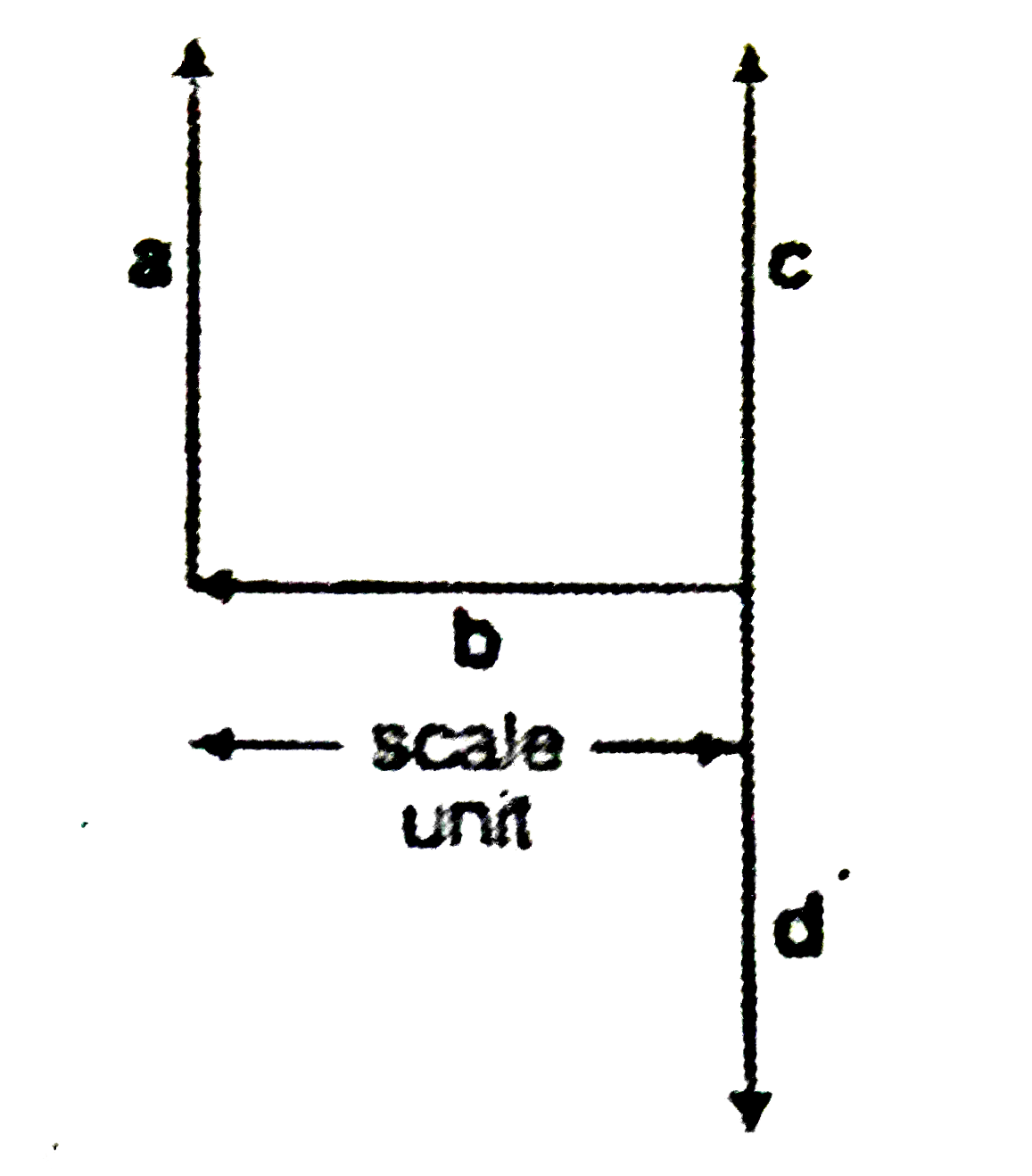
View SolutionIn a regular hexagon find which vectors are collinear, equal, coinitial, collinear but not equal.
View Solution

