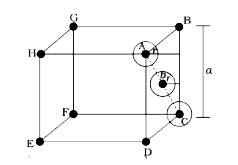
A metal crystallises in a face centred cubic structure. If the edge length of its unit cell is 'a' the closest approach between two atoms in metallic crystal will be
√2a
a√2
2a
2√2a
For fcc,
then b = 4r = √2a
a = 4r√2=2√2r⇒r=a2√2
Therefore, distance of closest approach
= 2r×a2√2=a√2
Similar Questions
A metal crystallises with a body-centred cubic lattice. The edge length of the unit cell is 360 pm. Radius of the metal atom is
View SolutionA metal crystallizes in a body centred cubic structure. If 'a' is the edge length of its unit cell, 'r' is the radius of the sphere. What is the relationship between 'r' and 'a' ?
View Solution
Knowledge Check
A metal crystallises in a face centred cubic structure. If the edge length of its cell is 'a' the closest approach between two atoms in metallic crystal will be
A2aB2√2aC√2aDa√2A metal crystallises in a face centred cubic structure. If the edge length of its cell is 'a' the closest approach between two atoms in metallic crystal will be
A2aB2√2aC√2aDa√2A metal crystallises in a face centred cubic structure. If the edge length of its unit cell is 'a' the closest approach between two atoms in metallic crystal will be
A2aB2√2aC√2aDa√2
A metal crystallises in a face centred cubic structure. If the edge length of its unit cell is 'a' the closest approach between two atoms in metallic crystal will be
View SolutionIn a face- centred cubic unit cell, the edge length is
View SolutionA metal crystallises in a simple cubic unit cell. If the edge length of the unit cell is 565.6 pm then, radius of metal atom is
View SolutionA metal crystallises in a simple cubic unit cell. If the edge length of the unit cell is 565.6 pm then, radius of metal atom is
View SolutionIn a face-centred cubic unit cell, edge length is
View Solution