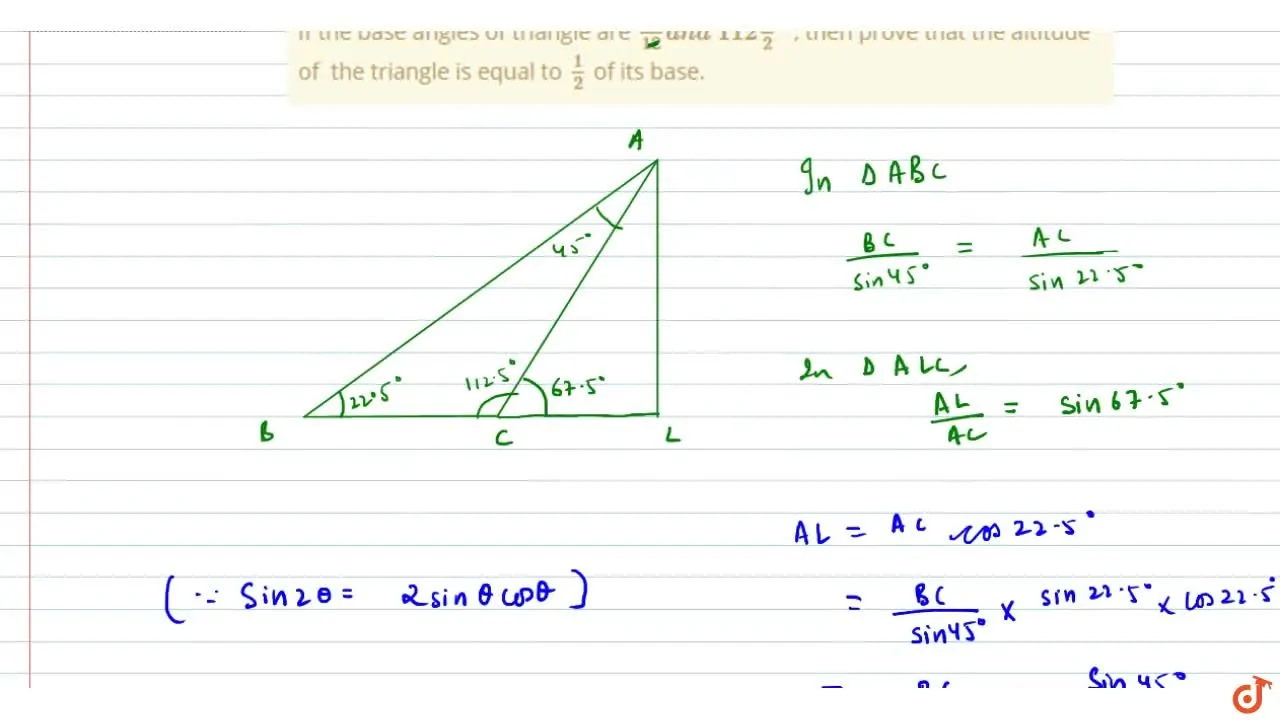
If the base angles of triangle are ${(\frac{22}{12})}^{\circ}$ and ${(112 \frac{1}{2})}^{\circ}$ , then prove that the altitude of the triangle is equal to $\frac{1}{2}$ of its base.

Video Solution

Text Solution

Verified by Experts

We can create a diagram with the given details.
Please refer to video to see the diagram.
$∠ B A C = 180 - 112.5 - 22.5 = 45^{\circ}$
$∠ A C L = 180 - 112.5 = {67.5}^{\circ}$
Now, in $Δ A B C$ ,
From sine law,
$\frac{B C}{{sin 45}^{\circ}} = \frac{A C}{{sin 22.5}^{\circ}}$
$\Rightarrow A C = \frac{B C {sin 22.5}^{\circ}}{{sin 45}^{\circ}}$
In $Δ A L C,$
$A L = A C {sin 67.5}^{\circ} = A C {cos 22.5}^{\circ}$
$\Rightarrow A L = \frac{B C {sin 22.5}^{\circ}}{{sin 45}^{\circ}} * {cos 22.5}^{\circ}$
$\Rightarrow A L = {sin 22.5}^{\circ} {cos 22.5}^{\circ} \cdot \frac{B C}{{sin 45}^{\circ}}$
$\Rightarrow A L = \frac{{sin 45}^{\circ}}{2} \cdot \frac{B C}{{sin 45}^{\circ}}$
$\Rightarrow A L = \frac{B C}{2}$
Therefore, altitude of the triangle is half of its base.

Updated on:21/07/2023

If the base angles of triangle are $\frac{22}{12} a n d 112 \frac{1}{2^{0}}$ , then prove that the altitude of the triangle is equal to $\frac{1}{2}$ of its base.
Abase
B $\frac{1}{3}$ rd of base
C $\frac{1}{2}$ of base
D $\frac{1}{4}$ th of base
Base of a right angled triangle is
A $\sqrt{{(Hypotenous)}^{2} + {(Perpendicular)}^{2}}$
B $\sqrt{{(Hypotenous)}^{2} - {(Perpendicular)}^{2}}$
C $\sqrt{{(Perpendicular)}^{2} - {(Hypotenous)}^{2}}$
DNone of These
If the area of a triangle is 1176 cm2 and base : corresponding altitude is 3 : 4, then the altitude of the triangle is (a) 42 cm (b) 52 cm (c) 54 cm (d) 56 cm
A42 m
B52 m
C54 m
D56 m