If →a,→band→c determine the vertices of a triangle, show that 12[→b×→c+→c×→a+→a×→d] givens the vector area of the triangle. Hence, deduce the condition that the three points →a,→band→c are collinera. Also, find the unit vector normal to the plane of the triangle.
The correct Answer is:Unit vector to the plane △ABC=→a×→b+→b×→c+→c×→a∣∣→a×→b+→b×→c+→c×→a∣∣
Step by step video & text solution for If veca,vecbandvecc determine the vertices of a triangle, show that (1)/(2)[vecbxxvecc+veccxxveca+vecaxxvecd] givens the vector area of the triangle. Hence, deduce the condition that the three points veca,vecband vecc are collinera. Also, find the unit vector normal to the plane of the triangle. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
If→a,→b,→c are the position vectors of the vertices A,B,C of a triangle ABC, show that the area triangle ABCis12∣∣→a×→b+→b×→c+→c×→a∣∣. Deduce the condition for points →a,→b,→c to be collinear.
View SolutionIf →a,→b,→c be three non coplanar vectors show that →b×→c,→c×→a,→a×→b are non coplanar.
View Solution
Knowledge Check
The vector area of triangle whose sides are →a,→b,→c is
A12∣∣→b×→c+→c×→a+→a×→b∣∣B12∣∣→b×→c+→c×→a+→b∣∣C13∣∣→b×→c+→c×→a+→b∣∣D12∣∣−→b×→c+→c×→a+→b∣∣In a righht angled triangle the three vectors →a,→b and →c add to zero. Then →a,→b is
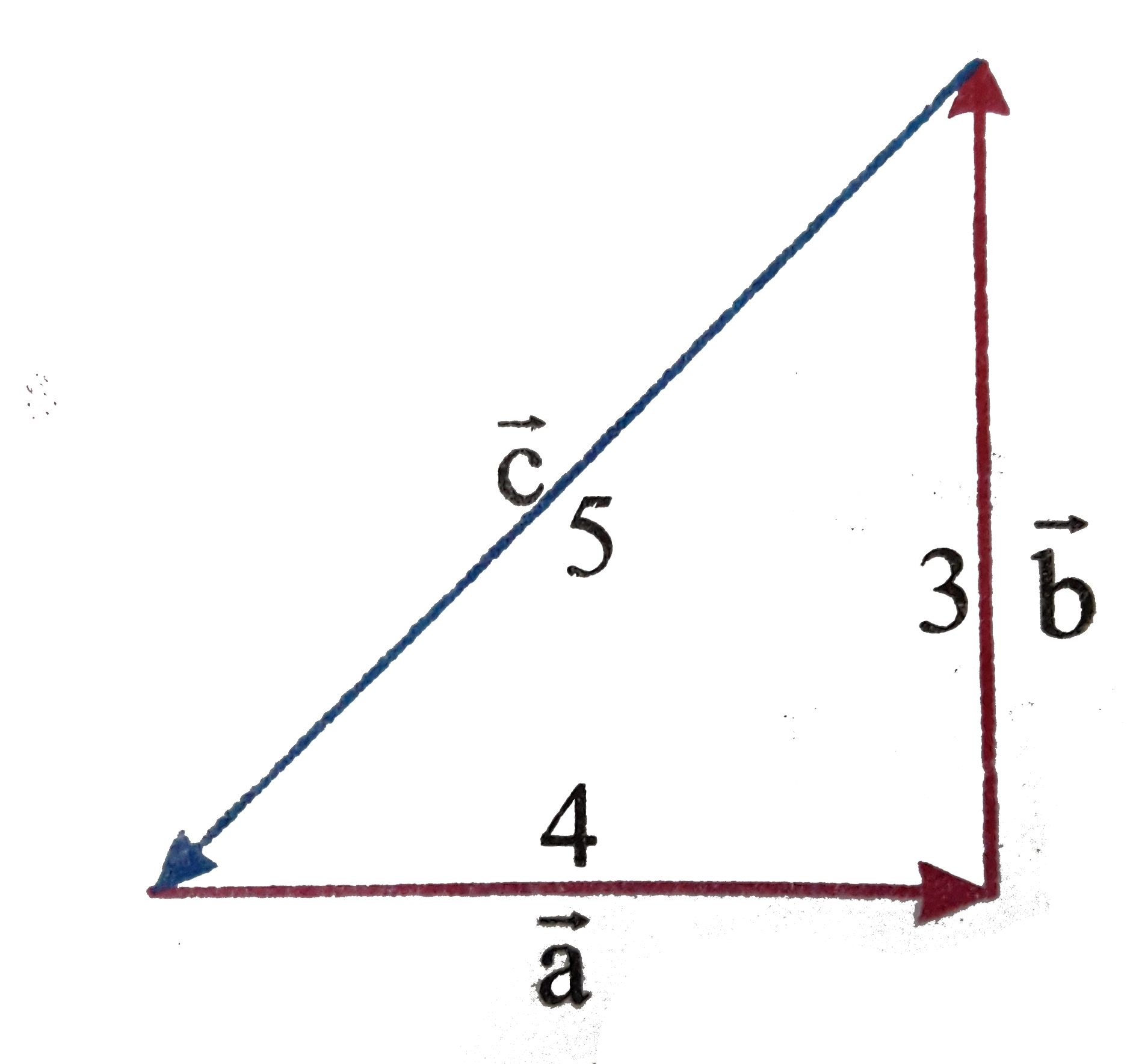 A−9B+9C0D−3
A−9B+9C0D−3If →a,→b,→c are the position vectors of the vertices. A,B,C of a triangle ABC. Then the area of triangle ABC is
A12∣∣→a×→b+→b×→c+→c×→a∣∣B12∣∣→a×→b∣∣C12∣∣→b×→c∣∣D12|→c×→a|
If →a,→band→c are the position vectors of vertices A,B,C of a ΔABC, show that the area of triangle ABC is 12∣∣→a×→b+→b×→c+→c×→a∣∣. Deduce the condition for points →a,→band→c to be collinear.
View SolutionA(1,2,5),B(5,7,9),andC(3,2,−1), are given three points. A unit Vector normal to the plane of the triangle ABC.
View SolutionLet →a,→b and →c be any three vectors; then prove that [→a×→b→b×→c→c×→a]=[→a→b→c]2
View SolutionFind the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0,−1),(2,1)and(0,3). Find the ratio of this area to the area of the given triangle.
View SolutionIF →a,→b,→c are the position vectors of the vertices of an equilateral triangle whose orthocentre is at the origin, then
View Solution