The largest area of the trapezium inscribed in a semi-circle or radius R, if the lower base is on the diameter, is 3√34R2 (b) √32R2 3√38R2 (d) R2
3√34R2
√32R2
3√38R2
R2
The correct Answer is:A
Step by step video & text solution for The largest area of the trapezium inscribed in a semi-circle or radius R , if the lower base is on the diameter, is (3sqrt(3))/4R^2 (b) (sqrt(3))/2R^2 (3sqrt(3))/8R^2 (d) R^2 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
The largest area of the trapezium inscribed in a semi-circle or radius R, if the lower base is on the diameter, is 3√34R2 (b) √32R2 3√38R2 (d) R2
View SolutionA cone is circumscribed about a sphere of radius R. The volume of the cone is minimum if its height is: (A) 3R (B) 4R (C) 5R (D) 2√2R
View Solution
Knowledge Check
The area of the largest triangle that can be inscribed in a semicircle of radius r is :
A2rcm2Br2cm2C2r2cm2D12r2cm2Three circles of radius 1 cm are circumscribed by a circle of radius r, as shown in the figure. Find the value of r?
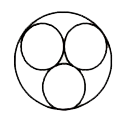
(a)√3+1
(b)2+√3√3
(c)√3+2√2
(d)2+√3A√3+1B2+√3√3C√3+2√2D2+√3
Prove that the least perimeter of an isosceles triangle in which a circle of radius r can be inscribed is 6√3r.
View SolutionA rectangle is inscribed in an equilateral triangle of side length 2a units. The maximum area of this rectangle can be √3a2 (b) √3a24 a2 (d) √3a22
View SolutionThe volume of the largest possible cube that can be inscribed in a hollow spherical ball of radius r cm is 2√3r2 (b) 43r2 (c) 83√3r3 (d) 13√3r3
View SolutionThree equal circles each of radius r touch one another. The radius of the circle touching all the three given circles internally is (2+√3)r (b) (2+√3)√3r (2−√3)√3r (d) (2−√3)r
View SolutionShow that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is 2R√3 .
View SolutionIn the given figure, ABC is an equilateral triangle which is inscribed inside a circle and whose radius is r . Which of the following is the area of the triangle? (r+DE)12(r−DE)32 (b) (r−DE)12(r+DE)2 (c) (r−DE)2(r+DE)2 (d) (r−DE)12(r+DE)32
View Solution
