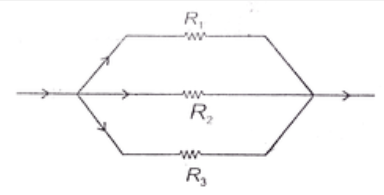
The possible percentage error in computing the parallel resistance R of three resistances 1R=1R1+1R21R3 from the formula , if R1,R2,R3 are each in error by plus 1.2% is :
0.012
0.013
0.014
0.015
The correct Answer is:A
To find the possible percentage error in computing the parallel resistance R of three resistances R1,R2,R3 when each resistance has an error of +1.2%, we can follow these steps:
Step 1: Write the formula for parallel resistance
The formula for the equivalent resistance R in parallel is given by:
1R=1R1+1R2+1R3
Step 2: Define the percentage error
The percentage error in a quantity X is defined as:
Percentage Error=ΔXX×100
where ΔX is the absolute error in X.
Step 3: Apply the error propagation formula
For the function 1R, the error propagation formula states:
⎛⎜
⎜⎝Δ(1R)1R⎞⎟
⎟⎠2=(ΔR1R1)2+(ΔR2R2)2+(ΔR3R3)2
Step 4: Substitute the known percentage errors
Given that each resistance R1,R2,R3 has a percentage error of +1.2%, we have:
ΔR1R1=ΔR2R2=ΔR3R3=0.012
Step 5: Calculate the total error in 1R
Substituting these values into the error propagation formula:
⎛⎜
⎜⎝Δ(1R)1R⎞⎟
⎟⎠2=(0.012)2+(0.012)2+(0.012)2
=3×(0.012)2=3×0.000144=0.000432
Step 6: Take the square root to find the error in 1R
Now, taking the square root gives:
Δ(1R)1R=√0.000432≈0.0208
Step 7: Convert to percentage error
To find the percentage error in R, we note that:
ΔRR=∣∣
∣
∣∣Δ(1R)1R∣∣
∣
∣∣
Thus, the percentage error in R is:
Percentage Error in R=ΔRR×100=0.0208×100≈2.08%
Final Answer
The possible percentage error in computing the parallel resistance R is approximately 2.08%.
---
The formula for the equivalent resistance R in parallel is given by:
1R=1R1+1R2+1R3
The percentage error in a quantity X is defined as:
Percentage Error=ΔXX×100
where ΔX is the absolute error in X.
For the function 1R, the error propagation formula states:
⎛⎜
⎜⎝Δ(1R)1R⎞⎟
⎟⎠2=(ΔR1R1)2+(ΔR2R2)2+(ΔR3R3)2
Given that each resistance R1,R2,R3 has a percentage error of +1.2%, we have:
ΔR1R1=ΔR2R2=ΔR3R3=0.012
Substituting these values into the error propagation formula:
⎛⎜
⎜⎝Δ(1R)1R⎞⎟
⎟⎠2=(0.012)2+(0.012)2+(0.012)2
=3×(0.012)2=3×0.000144=0.000432
Now, taking the square root gives:
Δ(1R)1R=√0.000432≈0.0208
To find the percentage error in R, we note that:
ΔRR=∣∣
∣
∣∣Δ(1R)1R∣∣
∣
∣∣
Thus, the percentage error in R is:
Percentage Error in R=ΔRR×100=0.0208×100≈2.08%
The possible percentage error in computing the parallel resistance R is approximately 2.08%.
Similar Questions
Knowledge Check
The possible percentage error in computing the parallel resistance R of three resistances R1,R2,R3 from the formula 1R=1R1+1R2+1R3, if R1,R2,R3 are each 1.2% in error, is
A1.2%B2.4%C0.6%D1.8%In parallel combination, the effective resistance (of R1 and R2) is given by
AR=R1R2R1+R2B1R=1R1+1R2CR=R1+R2DR=1R1+1R2A resistance R2 is connected in parallel with a resistance R1 what resistance R3 must be connected in series with the combination of R1andR2 so that the equivalent resistance is equal to the resistance R1 -
AR21R1+R2B(R1+R2)2R1CR22R1+R2DR21R2
Derive the relation 1R=1R1+1R2+1R3 when resistors are joined in parallel.
View Solutionprovetˆ:△ABC,1r1+1r2+1r3=1r
View SolutionWhen resistres of resistyences R1R2andR3 are connected in series , then the resistanceR1 is given by R1=R1+R2+R3
In this arrengement the current through each resister is same hut potential difference across then is difference
When resitorce of resistance R1R2andR3 are connected in particle the effective resistance Rp is given by 1Rp=1R1+1R2+1R3
In this arrangement , the potential difference across each resistance is but current through then is difference
Read the above passage and answer the following question :
(i) Why does the effective resistance increase in series ?
(ii) Why does the effective resistance decrease in parallel ?
(iii) What basic value are displayed by the above study ?
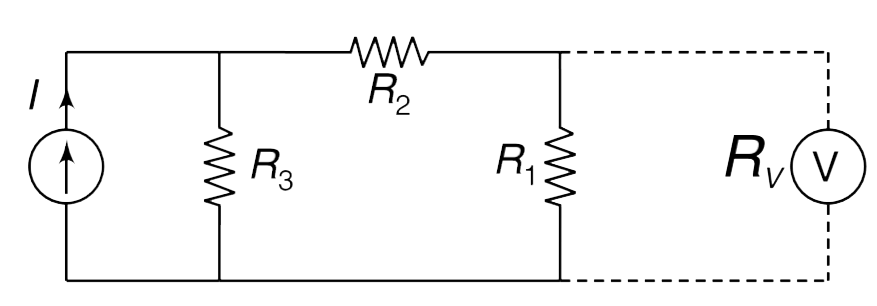
View SolutionThree resistors R1=3kΩ,R2=2kΩandR3=5kΩ have been connected to a constant current source as shown in figure. The current source supplies current I=2mA to the circuit. A voltmeter with RV=6kΩ internal resistance is connected, as shown, to measure the potential difference across R1.
(a) Find the percentage error in the measurement of potential difference (V1) across. R1 caused due to finite resistance of the voltmeter.
(b) If positions of R2andR3 are interchanged will the percentage error in measurement of V1 increase or decrease ?
View SolutionIf in a triangle (1−r1r2)(1−r1r3)=2, then the triangle is
View Solution