Let f(x) = [ n + p sin x], x∈(0,π),n∈Z, p a prime number and [x] = the greatest integer less than or equal to x. The number of points at which f(x) is not not differentiable is :
p
p−1
2p+1
2p−1
The correct Answer is:D
Step by step video & text solution for Let f(x) = [ n + p sin x], x in (0,pi), n in Z, p a prime number and [x] = the greatest integer less than or equal to x. The number of points at which f(x) is not not differentiable is : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
Let |x| be the greatest integer less than or equal to x, Then f(x)=xcos(π(x+[x]) is continous at
Ax=−1Bx=0Cx=2Dx−1 - Question 2 - Select One or More
Let [x] denotes the greatest integer less than or equal to x. If f(x)=[xsinπx], then f(x) is
Acontinuous at x = 0Bcontinuous in (−1,0)Cdifferentiable at x = 1Ddifferentiable in (−1,1) - Question 3 - Select One or More
Let [x] denotes the greatest integer less than or equal to x. If f(x)=[xsinπx], then f(x) is
Acontinuous at x=0,Bcontinuous in (-1,0),Cdifferentiable at x = 1Ddifferentiable in (-1,1),
If f(x)=|x−1|−[x] (where [x] is greatest integer less than or equal to x) then.
View SolutionIf f(x)=|x−1|−[x], where [x] is the greatest integer less than or equal to x, then
View SolutionLet f(x)=[cosx+sinx], 0<x<2π, where [x] denotes the greatest integer less than or equal to x. The number of points of discontinuity of f(x) is
View SolutionLet [x] denotes the greatest integer less than or equal to x. If f(x)=[xsinπx], then f(x) is
View SolutionLet [x] be the greatest integer less than or equal to x, for a real number x. Then the following sum
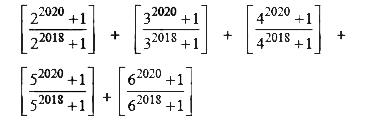
is-View Solution
