If the ratio of magnetic fields at two point in a definite direction due to a long current carrying wire is 3/4, then the ratio of the distances of these points from the wire will be :
2√3
43
√34
√32
The correct Answer is:B
Step by step video, text & image solution for If the ratio of magnetic fields at two point in a definite direction due to a long current carrying wire is 3/4, then the ratio of the distances of these points from the wire will be : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAGNETISM -1Book:MOTIONChapter:MAGNETISM -1Exercise:Exercise - 1 SECTION -E :- torque on a current carrying loop and magnetic dipole moment
Explore 13 Videos
- MAGNETISM -1Book:MOTIONChapter:MAGNETISM -1Exercise:Exercise - 2
Explore 30 Videos
- MAGNETISM -1Book:MOTIONChapter:MAGNETISM -1Exercise:Exercise - 1 SECTION -B :- Magnetic field due to cylinder
Explore 11 Videos
- MAGNETISM Book:MOTIONChapter:MAGNETISM Exercise:EXERCISE-4 (LEVEL-II)
Explore 40 Videos
- MATTER WAVEBook:MOTIONChapter:MATTER WAVEExercise:EXERCISE 3 (SECTION B)
Explore 7 Videos
Similar Questions
Knowledge Check
The direction of magnetic field at a point due to an infinitely long wire carrying current is
Aparallel to the currentBantiparallel to the currentCalong the perpendicular drawn from a point on the wireDperpendicular to the plane containing the conductor and the pointThe strength of the magnetic field at a point r near a long straight current carrying wire is B. The field at a distance r2 will be
AB2BB4C2BD4BMagnetic field due to an infinite current carrying wire varies with the distance (r) from the wire as
ArBr2C1rD1r2
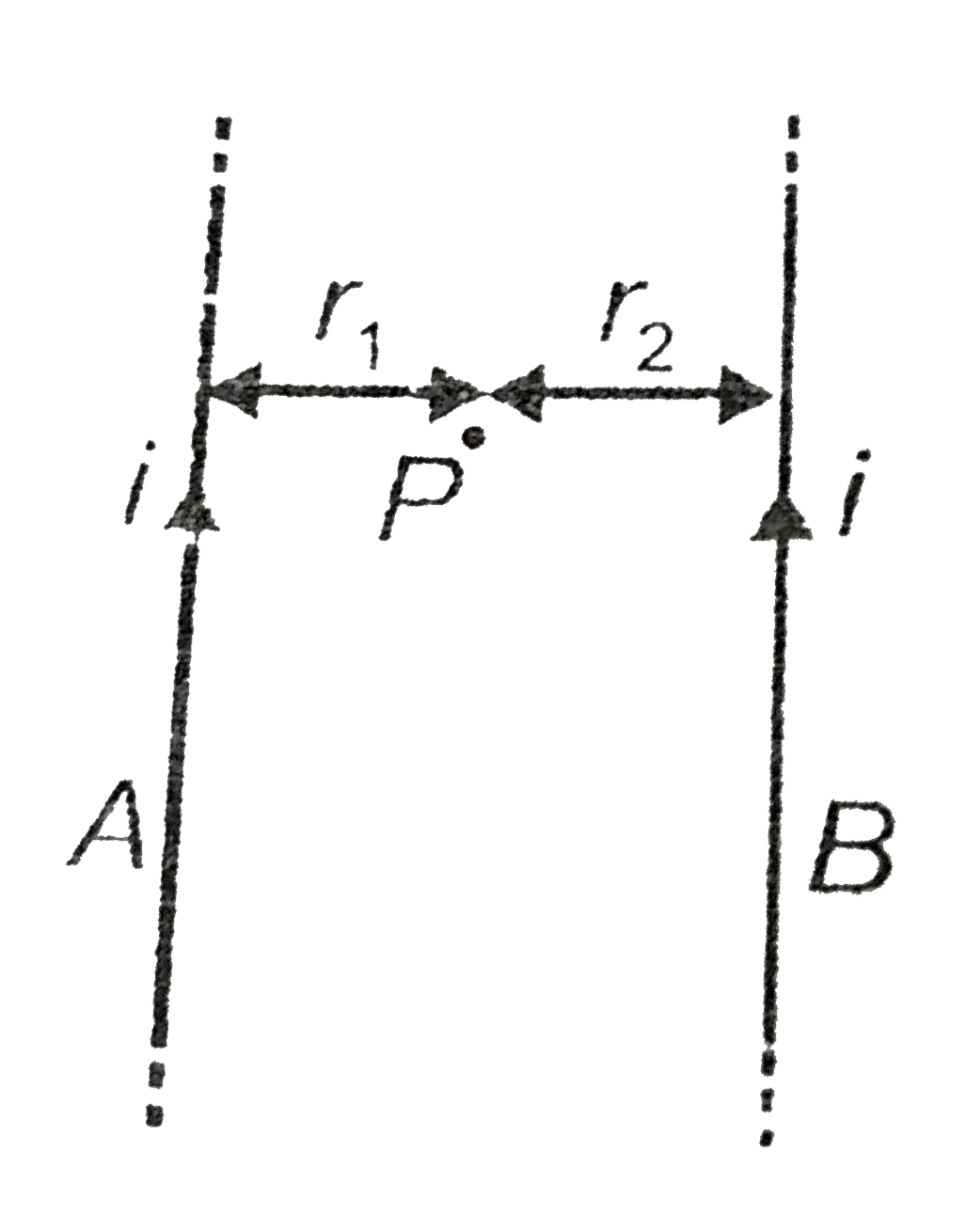
Find the direction of magnetic field at a point P due to two infinite current carrying wires shown in the figure. Given r1>r2
View SolutionMagnetic Field Created By Long Current Carrying Wire
View SolutionMagnetic field at a distance 'a' from long current carrying wire is proportional to -
View SolutionThe ratio of the magnetic field at the centre of a current carrying circular wire and the magnetic field at the centre of a square coil made from the same length of wire will be
View SolutionThe ratio of the magnetic field at the centre of a current carrying circular wire and the magnetic field at the centre of a semi-circular coil made from the same length of wire will be
View Solution

