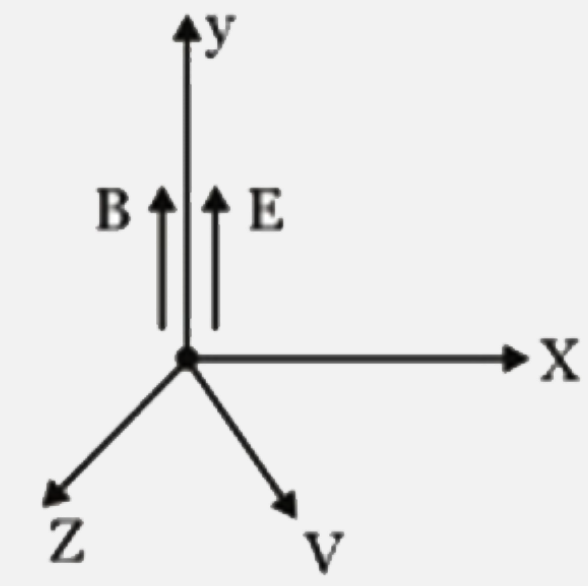
A charged particle of mass and charge has velocity . Find out the magnetic force on the charged particle and its acceleration at this instant due to magnetic field and are in and respectively.
Video Solution
Text Solution
By Newton 's Law
|
Topper's Solved these Questions
- MAGNETISM -1Book:MOTIONChapter:MAGNETISM -1Exercise:QUESTIONS FOR PRACTICE
Explore 34 Videos
- MAGNETISM -1Book:MOTIONChapter:MAGNETISM -1Exercise:Exercise - 1 SECTION -A :- Magnetif field due to straight wire
Explore 10 Videos
- MAGNETISM Book:MOTIONChapter:MAGNETISM Exercise:EXERCISE-4 (LEVEL-II)
Explore 40 Videos
- MATTER WAVEBook:MOTIONChapter:MATTER WAVEExercise:EXERCISE 3 (SECTION B)
Explore 7 Videos
Similar Questions
Knowledge Check
A charged particle has acceleration →a=2ˆi=xˆj in a magnetic field →B=−3ˆi+2ˆj−4ˆk.Find the value of x.
A4B2C6D3A charged particle of unit mass and unit charge moves with velocity →v=(8ˆi+6ˆj)ms−1 in magnetic field of →B=2ˆkT. Choose the correct alternative (s).
AThe path of the particle may be x2+y2−4x−21=0BThe path of the particle may be x2+y2=25CThe path of the particle may be y2+z2=25DThe time period of the particle will be 3.14sA charged particle moves with a velocity →v in a uniform magnetic field →B. The magnetic force experienced by the particle is
Aalways zeroBzero if →v and →B are perpendicularCnever zeroDzero if →v and →B are parallel or antiparallel.
A positive charge particle having change q and mass m has velocity →v=v(ˆi+ˆk√2) in the magnetic field B at the origin . Its speed as the function of y is :
View SolutionThe velocity of a particle is →v=3ˆi+2ˆj+3ˆk.Find the vector component of the velocity along the line ˆi−ˆj+ˆk and its magnitude.
View SolutionA charge q moves with a velocity 2m/s along x- axis in a unifrom magnetic field B=(ˆi+2ˆj+3ˆk) tesla.
View SolutionA charged particle moves in a magnetic field →B=10ˆi with initial velocity →u=5→i+4ˆj. The path of the particle will be
View SolutionIf →a=2ˆi−3ˆj−ˆk and →b=ˆi+4ˆj−2ˆk, then →a×→b is
View Solution