The tension of a piano wire is 16 Kg weight. What must be the change in tension so as to produce a tone an octave lower :
8kg weight
32 kg weight
12 kg weight
4 kg weight
The correct Answer is:C
To solve the problem, we need to determine the change in tension required to produce a tone that is an octave lower than the original tone produced by the piano wire.
1. Identify Given Data:
- Initial tension T1=16kg (weight)
- We need to find the new tension T2 that produces a tone an octave lower.
2. Understand the Relationship Between Frequency and Tension:
- The frequency of a vibrating string is given by the formula:
f=12L√Tμ
where L is the length of the string, T is the tension, and μ is the mass per unit length of the string.
3. Frequency Change for an Octave:
- A tone an octave lower means the frequency is halved. Therefore, if the original frequency is f1, the new frequency f2 will be:
f2=f12
4. Set Up the Ratio of Frequencies:
- From the frequency formula, we can set up the ratio:
f1f2=√T1√T2
- Since f2=f12, we have:
f1f12=2
- Thus, we can write:
2=√T1√T2
5. Square Both Sides:
- Squaring both sides gives:
4=T1T2
6. Substitute Known Values:
- Substitute T1=16kg:
4=16T2
7. Solve for T2:
- Rearranging gives:
T2=164=4kg
8. Calculate Change in Tension:
- The change in tension ΔT is given by:
ΔT=T1−T2=16kg−4kg=12kg
Final Answer:
The change in tension required to produce a tone an octave lower is 12kg.
---
- Initial tension T1=16kg (weight)
- We need to find the new tension T2 that produces a tone an octave lower.
- The frequency of a vibrating string is given by the formula:
f=12L√Tμ
where L is the length of the string, T is the tension, and μ is the mass per unit length of the string.
- A tone an octave lower means the frequency is halved. Therefore, if the original frequency is f1, the new frequency f2 will be:
f2=f12
- From the frequency formula, we can set up the ratio:
f1f2=√T1√T2
- Since f2=f12, we have:
f1f12=2
- Thus, we can write:
2=√T1√T2
- Squaring both sides gives:
4=T1T2
- Substitute T1=16kg:
4=16T2
- Rearranging gives:
T2=164=4kg
- The change in tension ΔT is given by:
ΔT=T1−T2=16kg−4kg=12kg
The change in tension required to produce a tone an octave lower is 12kg.
Topper's Solved these Questions
- WAVE MOTION BOOK - MOTIONCHAPTER - WAVE MOTION EXERCISE - Exercise - 3 Section - A (Previous Years Problems)
11 Videos
- WAVE MOTION BOOK - MOTIONCHAPTER - WAVE MOTION EXERCISE - Exercise - 3 Section - B (Previous Years Problems)
7 Videos
- WAVE MOTION BOOK - MOTIONCHAPTER - WAVE MOTION EXERCISE - EXERCISE - 1 (Section - E :- standing Wave)
18 Videos
- VECTOR & CALCULUSBOOK - MOTIONCHAPTER - VECTOR & CALCULUSEXERCISE - EXERCISE -4 (LEVEL - II) PREVIOUS YEAR
15 Videos
- WAVE OPTICS BOOK - MOTIONCHAPTER - WAVE OPTICS EXERCISE - EXERCISE - 4 (Level - II) Previous Year | JEE Main
16 Videos
Similar Questions
A weight of 1.0 kg is suspended form the lower end of a wire of cross- section 10mm2. What is the magnitude and direction of stress produced in it ? Take g=9.8ms−2.
View SolutionA tuning fork of unknown frequency vibrates in unison with a wire of certain stretched under a tension of 5 kg f. It produces 6 beats per second with the same wire, when tension is changed to 4.5 kg f. Find the frequency of tuning fork.
View Solution
Knowledge Check
The tension in a piano wire is 10N. The tension ina piano wire to produce a node of double frequency is
A20NB40NC10ND120NWhat is the percentage change in the tension necessary in a somometer of fixed length to produce a note one octave lower (half of original frequency) than before?
A25%B50%C67%D75%A piano wire having a diameter of 0.90mm is replaced by another wire of the same material but with a diameter of 0.93mm.If the tension of the wire is kept the same , then the percentage change in the frequency of the fundamental tone is
A+3%B+3.2%C−3.2%D−3%
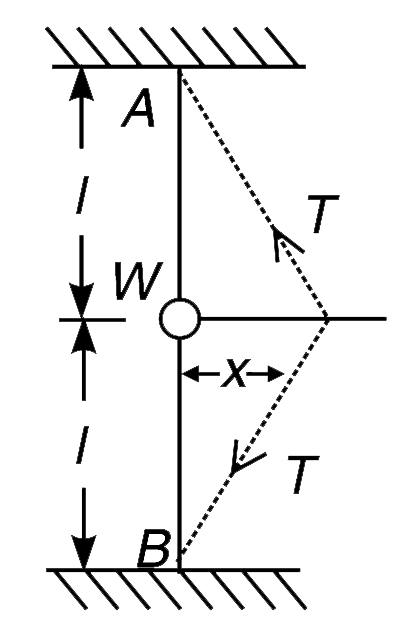
A small ball of mass m is attached to the middle of a tightly stretched perfectly flexible wire AB of length 2 l (figure ). The ball is given a small lateral displacement in horizontal direction and released. The initial tension (T) in the wire is high and change in it due to small lateral displacement of the ball can be neglected. Prove that the ball will perform simple harmonic motion, and calculate the period. If there is a device which can change the tension in the wire at will , how will the time period change if tension in the wire is increased
View SolutionThe frequency of a sonometer wire is 10Hz. When the weights producing the tension are completely immersed in water the frequency becomes 80Hz and on immersing the weights in a certain liquid the frequency becomes 60Hz. The specific gravity of the liquid is
View Solutionthe frequency of a sonometer wire is 10 Hz. When the weight producing th tensions are completely immersed in water the frequency becomes 80 Hz and on immersing the weight in a certain liquid the frequency becomes 60 Hz. The specific gravity of the liquid is
View Solutionthe frequency of a sonometer wire is 100 Hz. When the weight producing th tensions are completely immersed in water the frequency becomes 80 Hz and on immersing the weight in a certain liquid the frequency becomes 60 Hz. The specific gravity of the liquid is
View SolutionA transverse wave travels on a taut steel wire with a velocity of when tension in it is 2.06×104N . When the tension is changed to T, the velocity changed to 3v. The value of T is close to :
View Solution
