In a triangle ABC, ∠A=302,BC=2+√5, then find the distance of the vertex A from the orthocenter
A
1
B
(2+√5)√3
C
√3+12√2
D
12
Video Solution
Text Solution
The correct Answer is:B
|
Answer
Step by step video, text & image solution for In a triangle ABC, angle A = 30^(2), BC = 2 + sqrt5, then find the distance of the vertex A from the orthocenter by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - SOLUTION OF TRIANGLEEXERCISE - EXERCISE - 2 (LEVEL I)25videos
SOLUTION OF TRIANGLE
- BOOK - MOTIONCHAPTER - SOLUTION OF TRIANGLEEXERCISE - EXERCISE - 2 (LEVEL II)6videos
SOLUTION OF TRIANGLE
- BOOK - MOTIONCHAPTER - SOLUTION OF TRIANGLEEXERCISE - EXERCISE - 4( LEVEL II)10videos
SOLUTION OF TRIANGLE
- BOOK - MOTIONCHAPTER - SEQUENCE & SERIES EXERCISE - Exercise -4 Level -II Previous Year /JEE Advanced22videos
SEQUENCE & SERIES
- BOOK - MOTIONCHAPTER - STRAIGHT LINE EXERCISE - Exercise 4 Lelvel -II7videos
STRAIGHT LINE
Similar Questions
Knowledge Check
- Question 1 - Select One
In a triangle ABC, BC = √39, AC = 5 and AB = 7. What is the measure of the angle A?
Aπ4Bπ3Cπ2Dπ6 - Question 2 - Select One
In a triangle ABC,vertex angles A,B,C and side BC are given .The area of ΔABC is
As(s−a)(s−b)(s−c)2Bb2sinCsinAsinBCab sin CD12a2sinBsinCsinA - Question 3 - Select One
In ΔABCanl≥A=π6&b:c=2:√3then ∠B is
Aπ3Bπ2Cπ4DNon of these
Distance of the orthocenter H from vertex B is
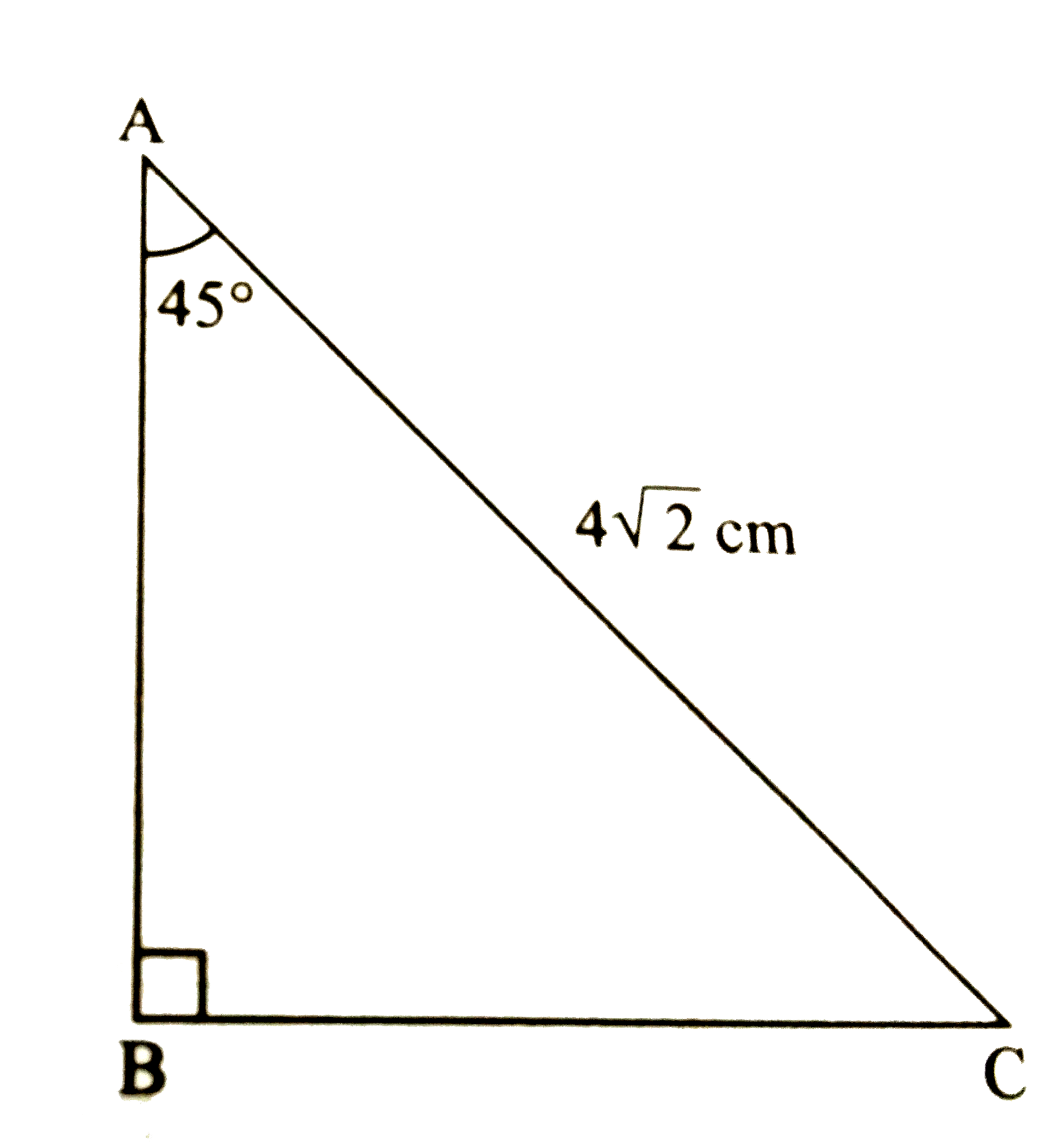
View SolutionIn △ABC,∠ABC=90∘
∠BAC=45∘ and AC =4√2cm,
then find AB.
 View Solution
View SolutionIn a ΔABC,∠B=90∘andAC=8√2. If AB=BC, then find AB.
View SolutionIn a triangle ABC, AB=BC and ∠A=60∘. Find ∠B.
View SolutionIn a triangle ABC if ∠ABC=60∘, then (AB−BC+CAr)2=
View Solution

