If 1 is the incentre and I1,I2,I3 are the centre of escribed circles of the △ABC. Prove that
II21+I2I23=II22+I3I21=I1I22+II23
The correct Answer is:II21+I2I23=II22+I3I21=I1I22+II23
Step by step video, text & image solution for If 1 is the incentre and I_1,I_2,I_3 are the centre of escribed circles of the triangleABC. Prove that II_(1)^(2)+I_2I_(3)^(2)= II_(2)^(2)+I_(3)I_(1)^(2)= I_(1)I_(2)^(2)+II_(3)^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SOLUTION OF TRIANGLEBOOK - MOTIONCHAPTER - SOLUTION OF TRIANGLEEXERCISE - EXERCISE -1
36 Videos
- SOLUTION OF TRIANGLEBOOK - MOTIONCHAPTER - SOLUTION OF TRIANGLEEXERCISE - EXERCISE - 2 (LEVEL I)
25 Videos
- SEQUENCE & SERIES BOOK - MOTIONCHAPTER - SEQUENCE & SERIES EXERCISE - Exercise -4 Level -II Previous Year /JEE Advanced
22 Videos
- STRAIGHT LINE BOOK - MOTIONCHAPTER - STRAIGHT LINE EXERCISE - Exercise 4 Lelvel -II
7 Videos
Similar Questions
Knowledge Check
The moment of inertia of thin square plate ABCD of uniform thickness about an axis passing through the center O and perpendicular to the plane of the plate is
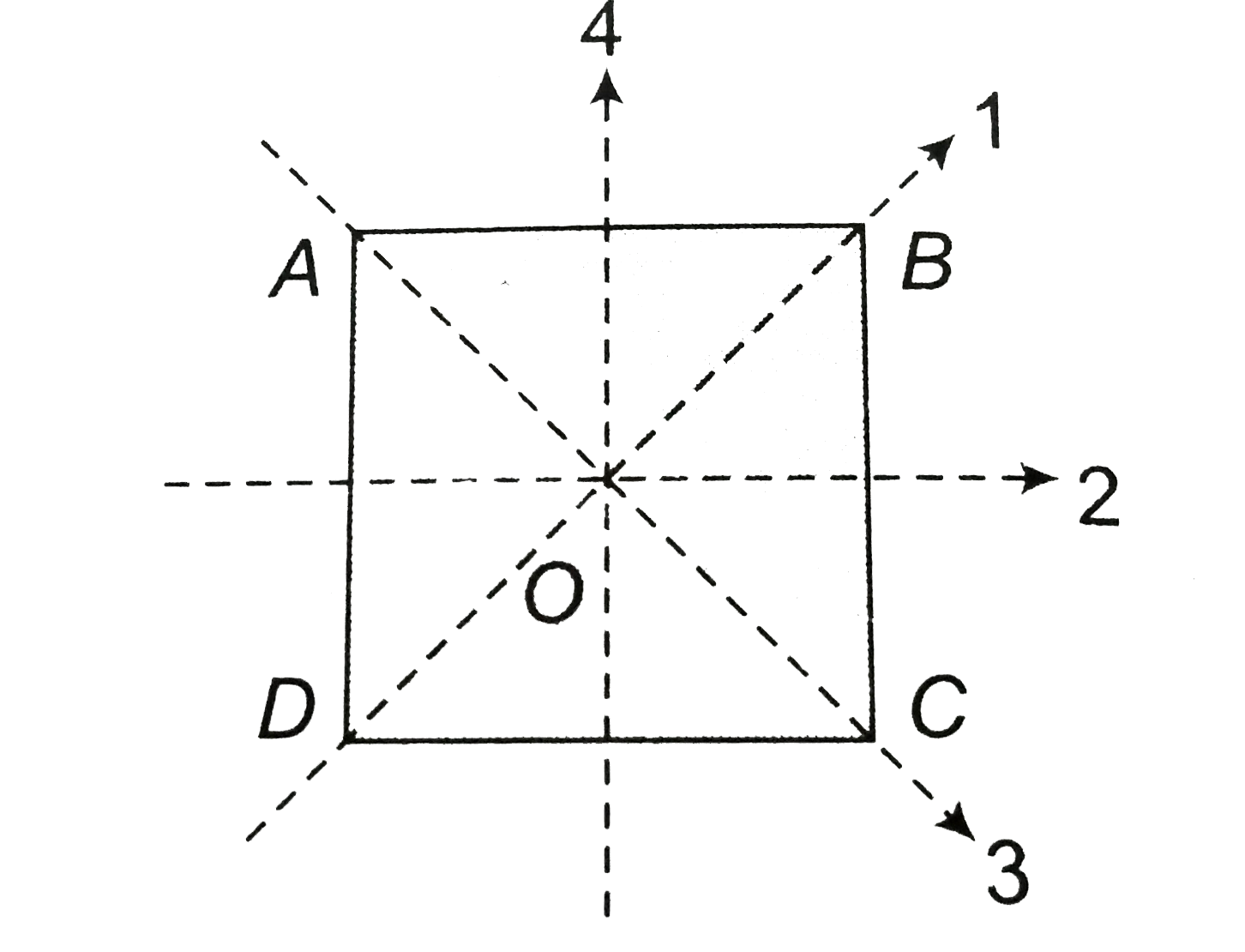
(i) I1+I2
(ii) I2+I4
(iii) I1+I3
(iv) I1+I2+I3+I4
where I1, I2, I3 and I4 are repectively moments of inertia about axes 1, 2, 3 and 4 which are in the plane of the planeA(i),(ii)B(i), (ii), (iii)C(ii), (iii)D(i), (iii)The moment of inertia of a thin square plate ABCD of uniform thickness about an axis passing through the centre O and perpendicular to the plane of the plate is
(a)I1+I2, (b)I2+I4
2I1+I3, (d) I1+2I3Aa,b are trueBb,c are trueCc,d are trueDb,d are true
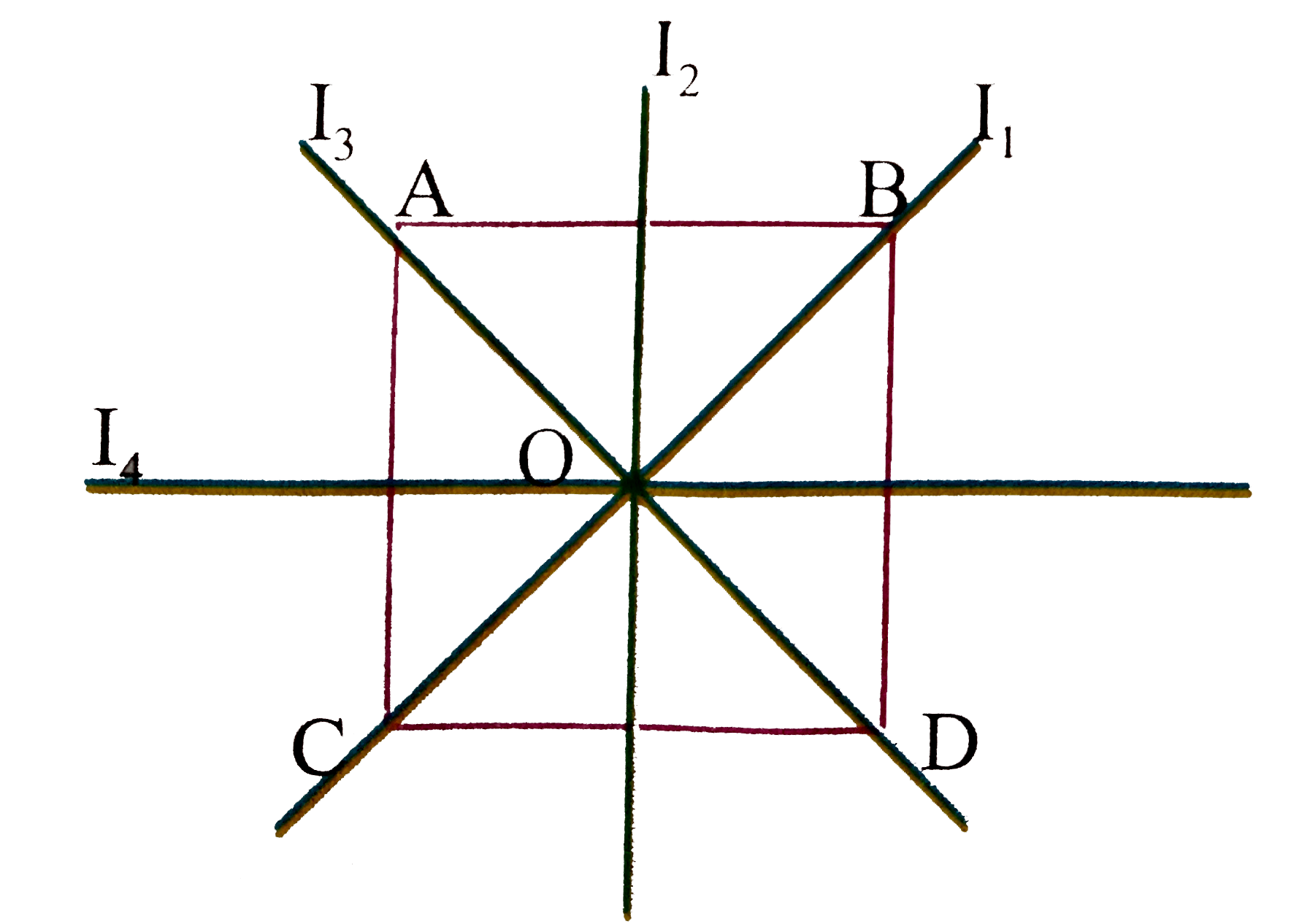
If I1,I2,I3 are the centers of escribed circles of ΔABC, show that the area of ΔI1I2I3 is (abc)/(2r)
View SolutionIn a triangle ABC I1,I2,I3 are excentre of triangle then show that II1.II2.II3=16R2r.
View SolutionIf I1,I2,I3andI are the excenter and incentres of ΔABC respectively, then (II1)).(II2).(II3)=
View Solution(−i)(2i)(−18i)3
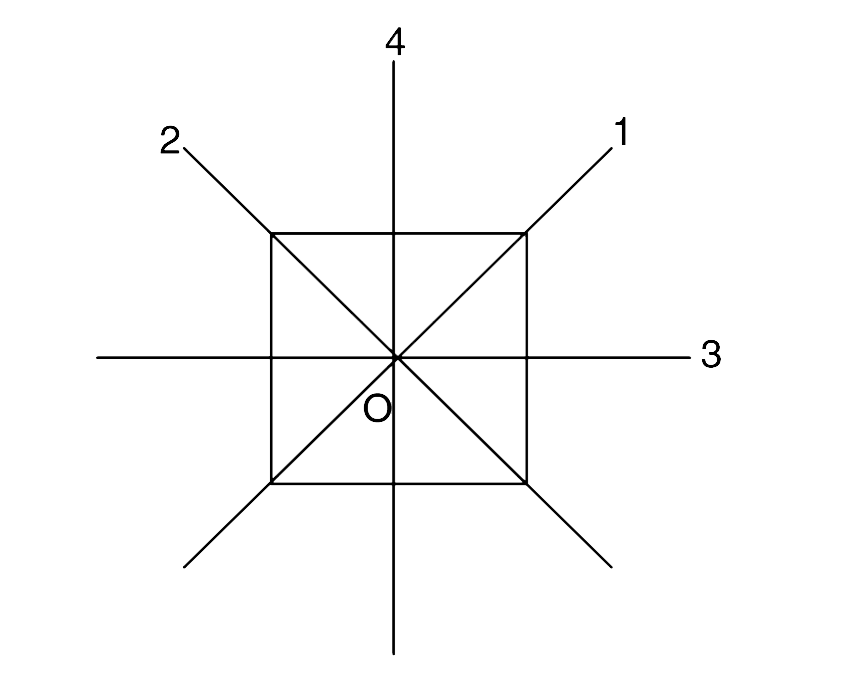
View SolutionConsider a uniform square plate shown in the figure. I1,I2,I3 and I4 are moment of inertia of the plate about the axes 1, 2, 3 and 4 respectively. Axes 1 and 2 are diagonals and 3 and 4 are lines passing through centre parallel to sides of the square. The moment of inertia of the plate about an axis passing through centre and perpendicular to the plane of the figure is equal to which of the followings.
(a) I3+I4
(b) I1+I3
(c) I2+I3
(d) 12(I1+I2+I3+I4)
View Solution(v)(1−i)2(1+i)−(3−4i)2
View Solution
