In a !ABC bisector of angle C meets the side AB at D and circumcricle at E. The maximum value of CD . DE is equal to
The correct Answer is:DE=a2sec(A)22(b+c).
Step by step video & text solution for In a !ABC bisector of angle C meets the side AB at D and circumcricle at E. The maximum value of CD . DE is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SOLUTION OF TRIANGLEBook:MOTIONChapter:SOLUTION OF TRIANGLEExercise:EXERCISE -1
Explore 36 Videos
- SOLUTION OF TRIANGLEBook:MOTIONChapter:SOLUTION OF TRIANGLEExercise:EXERCISE - 2 (LEVEL I)
Explore 25 Videos
- SEQUENCE & SERIES Book:MOTIONChapter:SEQUENCE & SERIES Exercise:Exercise -4 Level -II Previous Year /JEE Advanced
Explore 22 Videos
- STRAIGHT LINE Book:MOTIONChapter:STRAIGHT LINE Exercise:Exercise 4 Lelvel -II
Explore 7 Videos
Similar Questions
In ΔABC with fixed length of BC , the internal bisector of angle C meets the side AB at D and meet the circumcircle at E. The maximum value of CD×DE is
View SolutionIn ABC with fixed length of BC, the internal bisector of angle C meets the side ABatD and the circumcircle at E . The maximum value of CDxDE is c2 (b) c22 (c) c24 (d) none of these
View Solution
Knowledge Check
In a triangle ABC, angle bisector of ∠BAC cut the side BC at D and meet the circumcircle of ΔABC at E , then find AB .AC+DE. AE.
A2AEBAE2C2AE2D3AE2In a triangle ABC, angle bisector of ∠BAC cut the side BC at D and meet the circumcircle of ΔABC at E. If AC = 4 cm, AD = 5 cm, DE = 3 cm. Find the length of AB.
A10 cmB9.6 cmC12 cmD9 cmIn the triangle ABC, the internal bisector of angle A meets the side BC at D. If BD=7.5 cm and BC=9 cm. Then calculate the value of AB:AC.
A2 :1B1 :2C5 :1D1 :3
In ΔABC, the bisector of the angle A meets the sides BC at D and the circumscirbed circle at E. Prove that DE=a2sec.A22(b+c)
View SolutionIn a triangle ABC, angle bisector of ∠BAC cut the side BC at D and meet the circumcircle of ΔABC at E. If AC = 4 cm, AD = 5 cm, DE = 3 cm. Find the length of AB.
View SolutionIn triangle ABC,∠C=2π3andCD is the internal angle bisector of ∠C meeting the side AB at D. If Length CD is 1, then H.M. of aandb is equal to : (a) 1 (b) 2 (c) 3 (d) 4
View SolutionIn a triangle ABC, angle bisector of ∠BAC cut the side BD and meet the circumcircle of ΔABC at E. If AC = 4 cm, AD = 5 cm, DE = 3 cm. Find the length of AB.
View SolutionIn the given figure, ΔABC is inscribed in a circle and the bisector of ∠A meets BC in D and the circle in E. If ∠ECD=30∘, what is ∠A ?
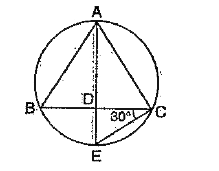
View Solution