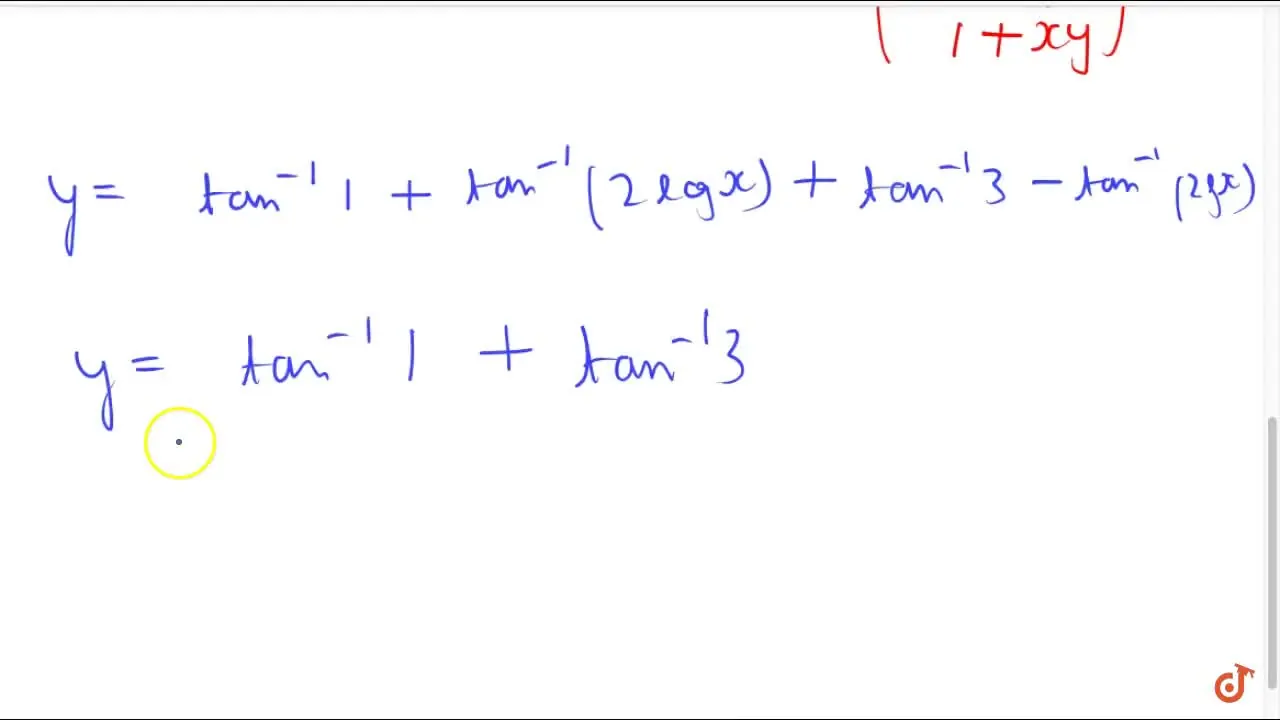If y=tan−1{(log)e(e/x2)(log)e(ex2)}+tan−1(3+2 (log)ex1−6 (log)ex) , then d2ydx2= (a) 2 (b) 1 (c) 0 (d) -1
dydx=0
d2ydx2=0
dydx=2x(1+In2x)
dydx=1
The correct Answer is:A, B
Step by step video, text & image solution for If y=tan^(-1){((log)_e(e//x^2))/((log)_e(e x^2))}+tan^(-1)((3+2\ (log)_e x)/(1-6\ (log)_e x)) , then (d^2y)/(dx^2)= (a) 2 (b) 1 (c) 0 (d) -1 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - MOTIONCHAPTER - METHOD OF DIFFERENTIATIONEXERCISE - EXERCISE - 325videos
METHOD OF DIFFERENTIATION
- BOOK - MOTIONCHAPTER - METHOD OF DIFFERENTIATIONEXERCISE - EXERCISE - 4 LEVEL -I6videos
METHOD OF DIFFERENTIATION
- BOOK - MOTIONCHAPTER - METHOD OF DIFFERENTIATIONEXERCISE - EXERCISE - 2 (LEVEL-I)17videos
METHOD OF DIFFERENTIATION
- BOOK - MOTIONCHAPTER - MAXIMA AND MINIMA EXERCISE - EXERCISE - 4 (LEVEL - II)17videos
MAXIMA AND MINIMA
- BOOK - MOTIONCHAPTER - MONOTONOCITYEXERCISE - Exercise - 4 ( Level-II ) Previous Year (Paragraph)2videos
MONOTONOCITY
Similar Questions
If y=tan−1{(log)e(e/x2)(log)e(ex2)}+tan−1(3+2 (log)ex1−6 (log)ex) , then d2ydx2= (a) 2 (b) 1 (c) 0 (d) -1
View SolutionIf y=tan−1⎧⎪ ⎪⎨⎪ ⎪⎩loge(ex2)loge(ex2)⎫⎪ ⎪⎬⎪ ⎪⎭+tan−1(3+2logex1−6logex), then d2ydx2=
View SolutionIf y=tan−1(log(e/x2)log(ex2))+tan−1(3+2logx1−6logx) then d2ydx2 is
View Solutionf(x)=tan−1⎧⎪ ⎪⎨⎪ ⎪⎩log(ex2)log(ex2)⎫⎪ ⎪⎬⎪ ⎪⎭+tan−−1(3+2logx1−6logx) then find dnydxn
View SolutionIf y=tan−1⎛⎜ ⎜⎝log(ex2)log(ex2)⎞⎟ ⎟⎠+tan−1(3+2logx1−6logx), then d2ydx2 is (a) 2 (b) 1 (c) 0 (d) −1
View SolutionIf y=tan−1[log(e/x3)log(ex3)]+tan−1[log(e4x3)log(e/x12)], then d2ydx2=
View SolutionIf y=tan−1(log(ex)log(ex)),thendydx=
View SolutionIf f(x)=cos−1{1−(logex)21+(logex)2}, then f'( e )
View SolutionIf y=∣∣(log)ex∣∣ , find d2ydx2 .
View SolutionIf y=tan−1[logexlog(ex)]+tan−1[8−logx1+8logx], then d2ydx2 is
View Solution