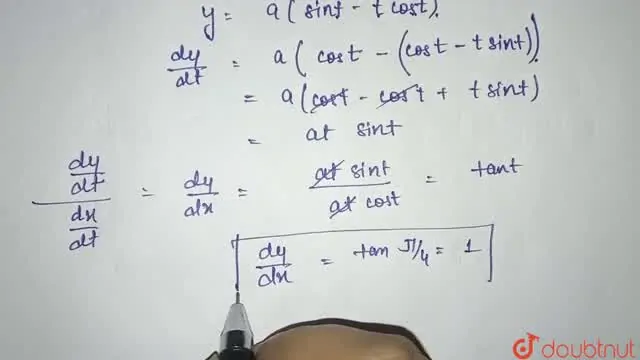If x = a (cos t + t sin t), y = a (sin t - t cos t),
then at t = $π / 4, \frac{d y}{d x}$

Video Solution

Answer

Step by step video & image solution for If x = a (cos t + t sin t), y = a (sin t - t cos t), then at t = pi//4,(dy)/(dx) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS CONTINUITY AND DIFFERENTIABILITY

Topper's Solved these Questions

METHOD OF DIFFERENTIATIONBook:MOTIONChapter:METHOD OF DIFFERENTIATIONExercise:EXERCISE - 1
Explore 27 Videos
METHOD OF DIFFERENTIATIONBook:MOTIONChapter:METHOD OF DIFFERENTIATIONExercise:EXERCISE - 2 (LEVEL-I)
Explore 17 Videos
MAXIMA AND MINIMA Book:MOTIONChapter:MAXIMA AND MINIMA Exercise:EXERCISE - 4 (LEVEL - II)
Explore 17 Videos
MONOTONOCITYBook:MOTIONChapter:MONOTONOCITYExercise:Exercise - 4 ( Level-II ) Previous Year (Paragraph)
Explore 2 Videos

Knowledge Check

If $x = a (t cos t - sin t), y = a (t sin t + cos t), t h e n \frac{d y}{d x} =$
A $- tan t$
B $tan t$
C $- cot t$
D $cot t$
The distance, from the origin, of the normal to the curve, $x = 2 cos t + 2 t sin t, y = 2 sin t - 2 t cos t at t = \frac{π}{4}$ , is :
A2
B4
C $\sqrt{2}$
D $2 \sqrt{2}$

MOTION-METHOD OF DIFFERENTIATION-EXERCISE - 4 LEVEL -II

Home
Ask Doubt
Profile

If x = a (cos t + t sin t), y = a (sin t - t cos t), then at t = π/4,dydx

Topper's Solved these Questions

Similar Questions

Knowledge Check

If x=a(tcost−sint),y=a(tsint+cost),thendydx=

The distance, from the origin, of the normal to the curve, x=2cost+2tsint,y=2sint−2tcos t at t=π4, is :

MOTION-METHOD OF DIFFERENTIATION-EXERCISE - 4 LEVEL -II

If x = a (cos t + t sin t), y = a (sin t - t cos t),
then at t = $π / 4, \frac{d y}{d x}$

If $x = a (t cos t - sin t), y = a (t sin t + cos t), t h e n \frac{d y}{d x} =$

The distance, from the origin, of the normal to the curve, $x = 2 cos t + 2 t sin t, y = 2 sin t - 2 t cos t at t = \frac{π}{4}$ , is :