A circular are of radius 1 subtends an angle of x radians 0<x<π2 as shown in the figure . the point r is the intersection of the two tangent line at P and Q. let T(x) be the area of triangle PQR and S(x) be the area of the shaded region then find T(x)&S(x)&limx→0T(x)S(x)
The correct Answer is:limit =32
Step by step video, text & image solution for A circular are of radius 1 subtends an angle of x radians 0 < x < pi/2 as shown in the figure . the point r is the intersection of the two tangent line at P and Q. let T(x) be the area of triangle PQR and S(x) be the area of the shaded region then find T(x) & S(x) & lim_(x->0)(T(x))/(S(x)) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LIMITBook:MOTIONChapter:LIMITExercise:EXERCISE-4
Explore 17 Videos
- LIMITBook:MOTIONChapter:LIMITExercise:EXERCISE-2(LEVEL-2)
Explore 5 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBook:MOTIONChapter:INVERSE TRIGONOMETRIC FUNCTIONSExercise:Exercise -4 Level -II
Explore 7 Videos
- MATRICES Book:MOTIONChapter:MATRICES Exercise:Exercise - 4 (Level-II)
Explore 28 Videos
Similar Questions
A circle arc of radius 1 subtends an angle of x radians as shown in figure. The centre of the circle is O and the point C is the intersection of two tangent lines at A and B. Let T(x) be the area of ΔABC and S(x) be the area of shaded region.
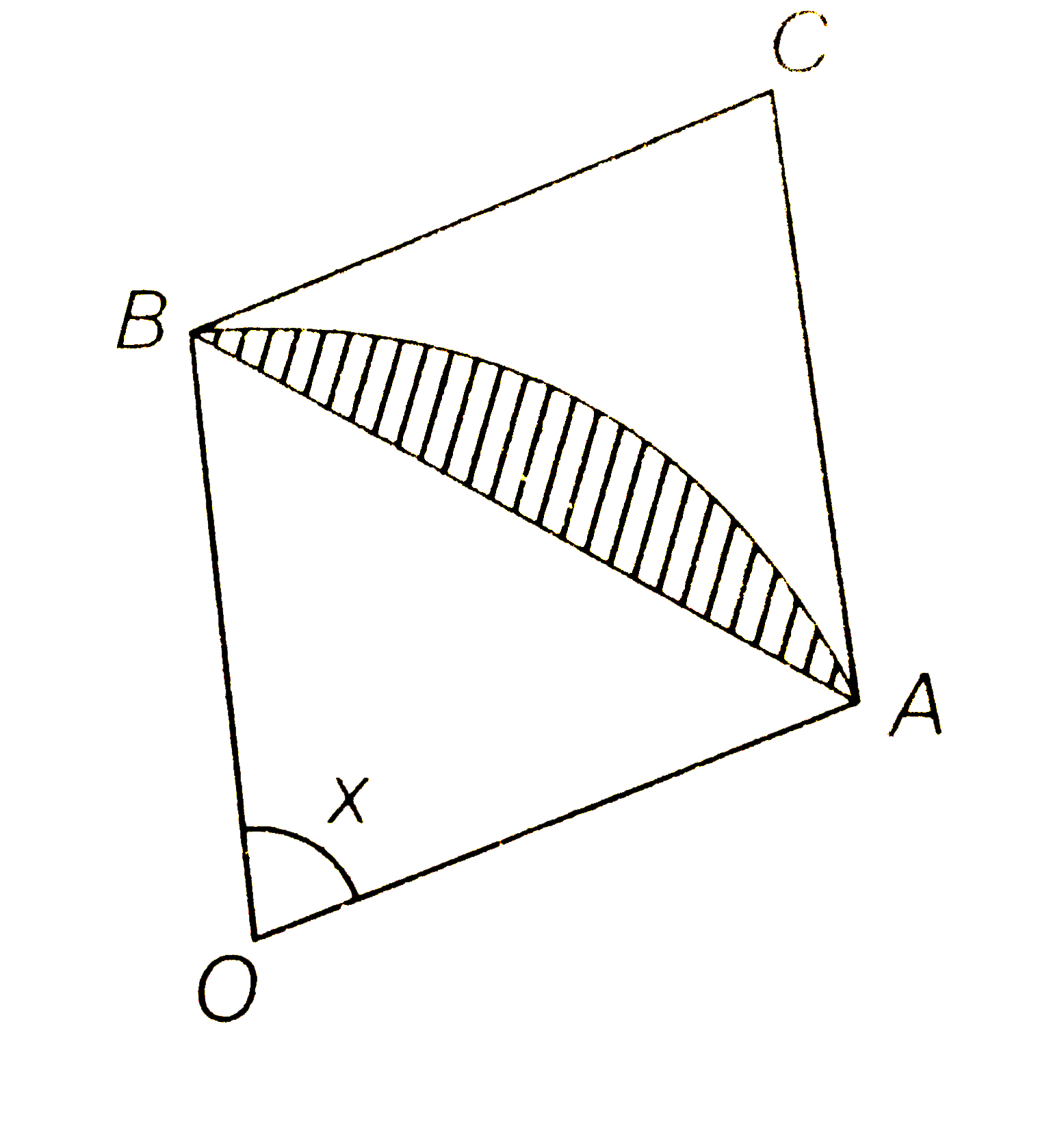
limx→0T(x)x3 is
View SolutionA circle arc of radius 1 subtends an angle of x radians as shown in figure. The centre of the circle is O and the point C is the intersection of two tangent lines at A and B. Let T(x) be the area of ΔABC and S(x) be the area of shaded region.
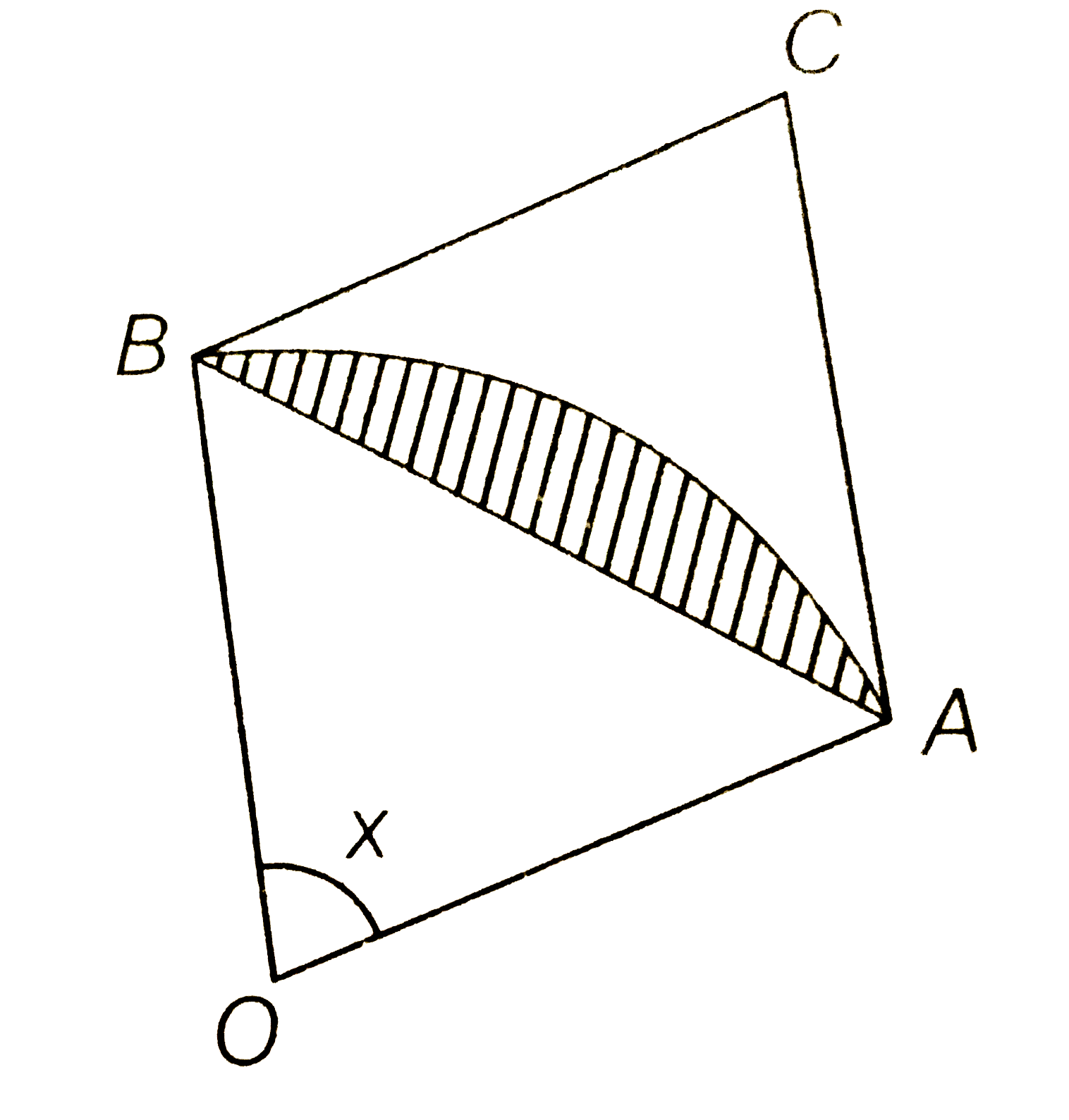
limx→0S(x)x is
View Solution
Knowledge Check
A mirror produces on a screen an image of the sun 2cm in diameter. If the sun's disc subtends an angle 0.1 radian on the surface of the earth, then the radius of curvature of the mirror is
A20cmB40cmC200cmD400cm
A circular arc of wire of radius of curvature r subtends an angle of p/4 radian at its centre. If i current is flowing in it then the magnetic induction at its centre is -
View SolutionA circle are PQ of radius an angle s radius 0<x<π2 point R is the point of intersection of tangents at PandQ on the are Let T(x) be the area of ΔPQR,S(x) be the area of setor OPQ and T(x) be area of ΔOPQ
View SolutionAn arc of length 10cm of a circle of radius 5cm subtends an angle at the center is equal to ( in radians)
View SolutionA circular arc of length π cm. Find angle subtended by it at the centre in radian and degree.
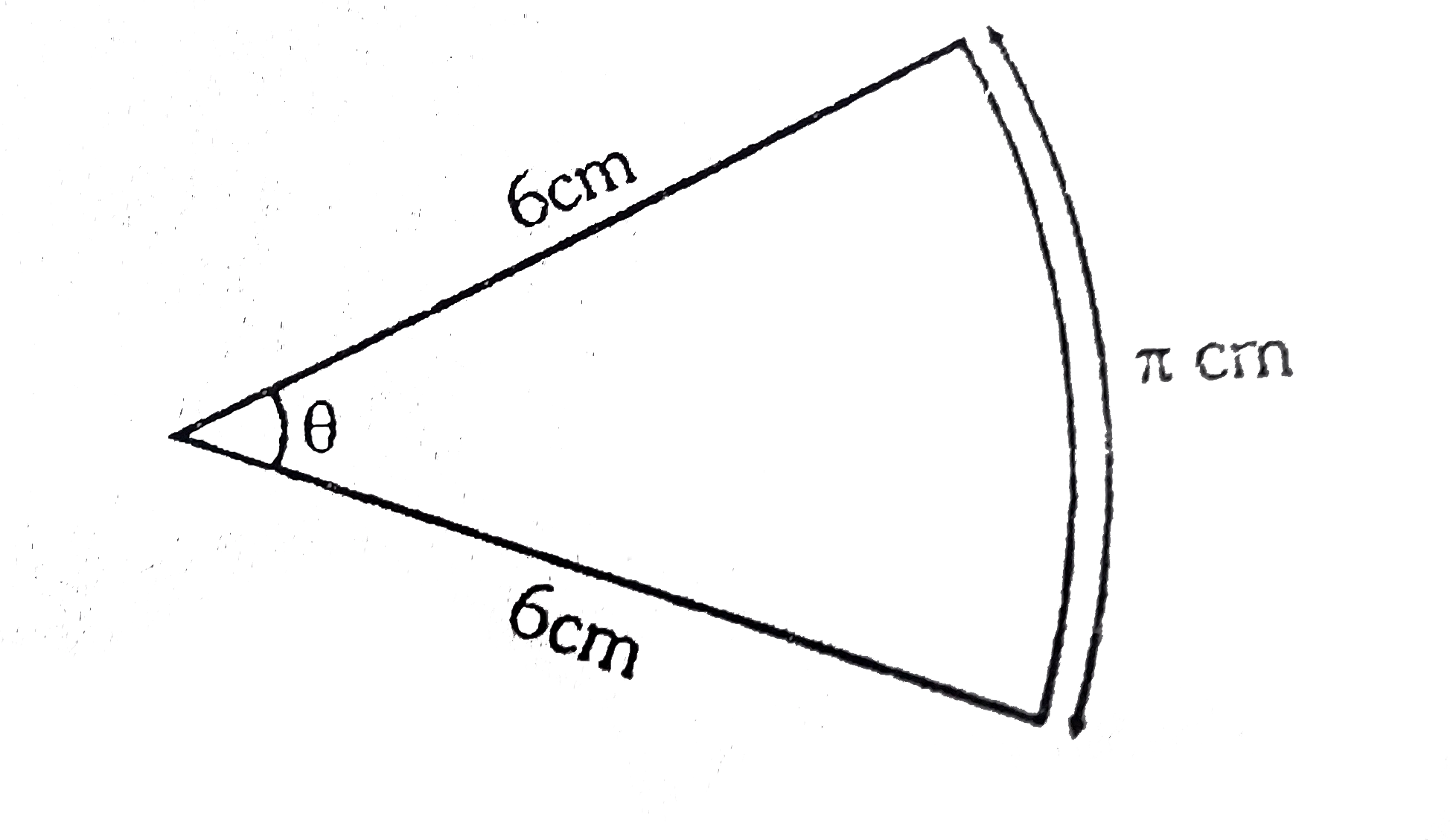
View SolutionA constant magnetic field of 1 T is applied in the x>0 region. A metallic circular ring of radius 1 m is moving with a constant velocity of 1 m/s along the x-axis. At t=0 s, the centre O of the ring is at x=-1 m. What will be the value of the induced emf in the ring at t=1s? (Assume the velocity of the ring does not change.)
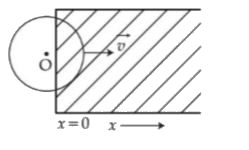
View SolutionIf α1andα2 be the circular measures of the angles subtended by the arcs of lengths S1,S2 at the centres of the circles whose radii are a1,a2 respectively, then show that the angle subtended at the centre by the arc of length (s1+s2) of a circle whose radius is 1n(a1α1+a2α2) will be n radians.
View SolutionConsider the following statements :
1. The angular measure in radian of a
circular arc of fixed length subtending
at its centre decreases if the radius of
the arc increases.
2. 1800∘ is equal to 5π radian .
Which of the statements is/are correct ?
View Solution

