The graph of the function f(x)=Limt→0(2xπcot−1xt2), is
A
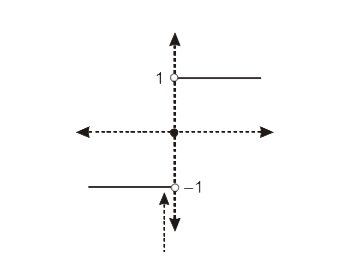
B
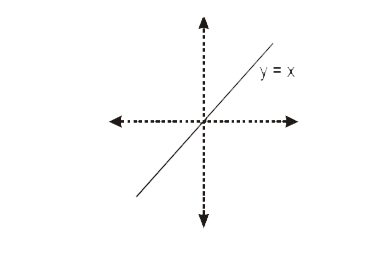
C
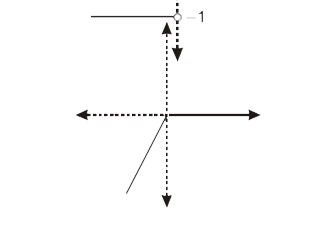
D
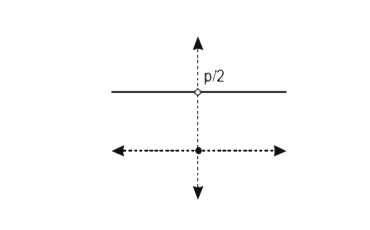
Video Solution
Text Solution
The correct Answer is:C
|
Answer
Step by step video, text & image solution for The graph of the function f(x) = underset( t rarr 0 ) ("Lim") ((2x)/(pi ) cot^(-1) ""(x) /(t^(2))), is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LIMITBook:MOTIONChapter:LIMITExercise:EXERCISE -2( LEVEL-I)
Explore 16 Videos
- LIMITBook:MOTIONChapter:LIMITExercise:EXERCISE-2(LEVEL-2)
Explore 5 Videos
- LIMITBook:MOTIONChapter:LIMITExercise:EXERCISE-4
Explore 17 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBook:MOTIONChapter:INVERSE TRIGONOMETRIC FUNCTIONSExercise:Exercise -4 Level -II
Explore 7 Videos
- MATRICES Book:MOTIONChapter:MATRICES Exercise:Exercise - 4 (Level-II)
Explore 28 Videos
Similar Questions
Knowledge Check
limx→0xtan2x−2xtanx(1−cos2x)2 is
A2B−2C12D−12limx→0(cot(π4+x))cosecx=
Ae−1Be2Ce−2De1If l=Limx→0x(1+acosx)−bsinxx3=Limx→01+acosxx2−limx→0bsinxx3 , where l∈R, then
A(a,b)=(−1,0)Ba & b are nay real numbersCl = 0Dl=12
Plot the graph of the function f(x)=limt→0(2xπtan−1xt2)
View SolutionEvaluate Limx→0ex−e−x−2xx−sinx
View Solutionf(x) is the function such that Limx→0f(x)x=1.
If Limx→0x(1+acosx)−bsinx(f(x))3=1 , then find the value of a and b.
View SolutionIf f(x)=limt→0[2xπ.tan−1(xt2)],then f(1) is …….
View SolutionIf f(2010)=π/2,f(2x)=f(x)∀x∈R and f(x) is continuous for x∈R, then the value of limx→0cos(f(x))−3√cos(f(x))sin2x is Limx→π/2[x−π2cosx] is
View Solution

