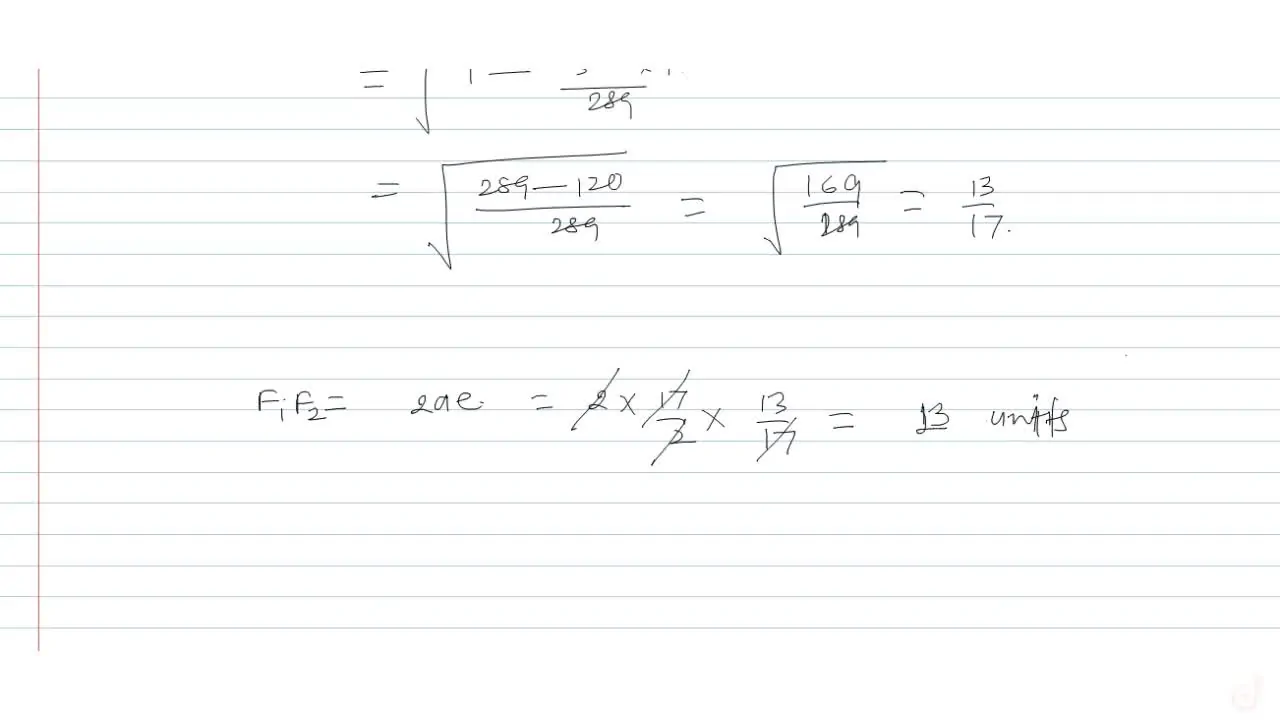A circle has the same center as an ellipse and passes through the foci F1andF2 of the ellipse, such that the two cuves intersect at four points. Let P be any one of their point of intersection. If the major axis of the ellipse is 17 and the area of triangle PF1F2 is 30, then the distance between the foci is 13 (b) 10 (c) 11 (d) none of these
12
13
14
15
The correct Answer is:C, D
Step by step video, text & image solution for A circle has the same center as an ellipse and passes through the foci F_1a n dF_2 of the ellipse, such that the two cuves intersect at four points. Let P be any one of their point of intersection. If the major axis of the ellipse is 17 and the area of triangle P F_1F_2 is 30, then the distance between the foci is 13 (b) 10 (c) 11 (d) none of these by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - MOTIONCHAPTER - ELLIPSE EXERCISE - Exercise - 3 | Subjective | JEE Advanced21videos
ELLIPSE
- BOOK - MOTIONCHAPTER - ELLIPSE EXERCISE - Exercise - 4 | Level-I Previous Year | JEE Main20videos
ELLIPSE
- BOOK - MOTIONCHAPTER - ELLIPSE EXERCISE - Exercise - 2 (Level-I) Objective Problems | JEE Main13videos
ELLIPSE
- BOOK - MOTIONCHAPTER - DIFFERENTIAL EQUATION EXERCISE - Exercise 429videos
DIFFERENTIAL EQUATION
- BOOK - MOTIONCHAPTER - FUNCTIONEXERCISE - Exercise - 4 | Level-II7videos
FUNCTION
Similar Questions
A circle has the same center as an ellipse and passes through the foci F1andF2 of the ellipse, such that the two cuves intersect at four points. Let P be any one of their point of intersection. If the major axis of the ellipse is 17 and the area of triangle PF1F2 is 30, then the distance between the foci is (a)13 (b)10 (c)11 (d) none of these
View SolutionA circle concentric with the ellipse x2a2+y2b2=1 and passes through the foci F1andF2 of the ellipse. Two curves intersect at fur points. Let P be any point of intersection. If the major axis of the ellipse is 15 and the area of triangle PF1F2 is 26, then find the valueof 4a2−4b2.
View SolutionA circle has same centre as an ellipse and passing through foci S1 and S2 of the ellipse. The two curves cut in four points. Let P be one of the points. If the Area of △PS1S2 is 24 and major axis of the ellipse is 14. If the eccentricity of the ellipse is e, then the value of 7e is equal to
View SolutionAn ellipse having foci (3,1) and (1,1) passes through the point (1,3) has the eccentricity
View SolutionAn ellipse has foci (4, 2), (2, 2) and it passes through the point P (2, 4). The eccentricity of the ellipse is
View SolutionFind the equation of the ellipse that passes through the origin and has the foci at the points (−1,1)andS'(1,1).
View SolutionAn ellipse is sliding along the coordinate axes. If the foci of the ellipse are (1, 1) and (3, 3), then the area of the director circle of the ellipse (in square units) is 2π (b) 4π (c) 6π (d) 8π
View SolutionLet P be a variable point on the ellipse x2a2+y2b2=1 with foci F1 and F2. If A is the area of the △PF1F2, then the maximum value of A is
View SolutionThe ellipse 4x2+9y2=36 and the hyperbola 4x2–y2=4 have the same foci and they intersect at right angles then the equation of the circle through the points of intersection of two conics is
View SolutionP is a variable point on the ellipse with foci S1 and S2. If A is the area of the the triangle PS1S2, the maximum value of A is
View Solution