It is known that the decay rate of radium is directly proportional to its quantity at each given instant. Find the law of variation of a mass of radium as a function of time if at t=0, the mass of the radium was m0 and during time t0 α% of the original mass of radium decay.
The correct Answer is:m=m0e−ktwherek=−1t∘ln(1−α100)
Step by step video & text solution for It is known that the decay rate of radium is directly proportional to its quantity at each given instant. Find the law of variation of a mass of radium as a function of time if at t=0, the mass of the radium was m_0 and during time t_0 alpha% of the original mass of radium decay. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIAL EQUATION Book:MOTIONChapter:DIFFERENTIAL EQUATION Exercise:Exercise 4
Explore 29 Videos
- DIFFERENTIAL EQUATION Book:MOTIONChapter:DIFFERENTIAL EQUATION Exercise:Exercise 2
Explore 48 Videos
- DIFFERENTIABILITYBook:MOTIONChapter:DIFFERENTIABILITYExercise:Exercise - 4 | Level-I Previous Year | JEE Main
Explore 15 Videos
- ELLIPSE Book:MOTIONChapter:ELLIPSE Exercise:Exercise - 4 | Level-I Previous Year | JEE Main
Explore 20 Videos
Similar Questions
The decay rate of radium at any time t is proportional to its mass at that time. Find the time when the mass will be halved of its initial mass.
View SolutionA body of mass m, accelerates uniformly from rest to v1 in time t1. Find the instantaneous power delivered to the body as a function of time t.
View Solution
Knowledge Check
A certain mass of radium is reduced by 70% in 2780 years. The decay constant is
A4.3×10−4 per yearB3.4×10−4 per yearC5.4×10−4 per yearD4.8×10−4 per yearSuppose a rocket with an intial mass M0 eject a mass Δm in the form of gases in time Δt, then the mass of the rocket after time t is :-
AM0−ΔmΔt.tBM0−ΔmΔtCM0−ΔmΔtDM0Work done in time t on a body of mass m which is accelerated from rest to a speed v in time t1 as a function of time t is given b
A12mvt1t2Bmvt1t2C12(mvt1)2t2D12mv2t21t2
Radium decomposes at a rate proportional to the quantity of radium present. It is found that in 25 years, approximately 1⋅1 precent of a certain quantity of radium has decomposed. Determine approximately how long it will take for one-half of the original amount of radium to decompose ?
(loge0.989=−0⋅01106,loge2=0⋅6931)
View SolutionThe rate of disintegration of a radioactive element at any time t is proportional to its mass at that time. Find the time during which the original mass of 1.5 g m will disintegrate into its mass of 0.5 gm.
View SolutionA certain radioactive material is known to decay at a rate proportional to the amount present. If initially there is 50 kg of the material present and after two hours it is observed that the material has lost 10% of its original mass, find () and expression for the mass of the material remaining at any time t, (ii) the mass of the material after four hours and (iii) the time at which the material has decayed to one half of its initial mass.
View SolutionHalf-life of radium is 1,620 years. After how many years 0.75 mg of radium will be disintegrated out of its initial mass of 1 mg.
View SolutionShows position time graph of a particle of mass 100g Find the impulse at t=0 and at t=4s
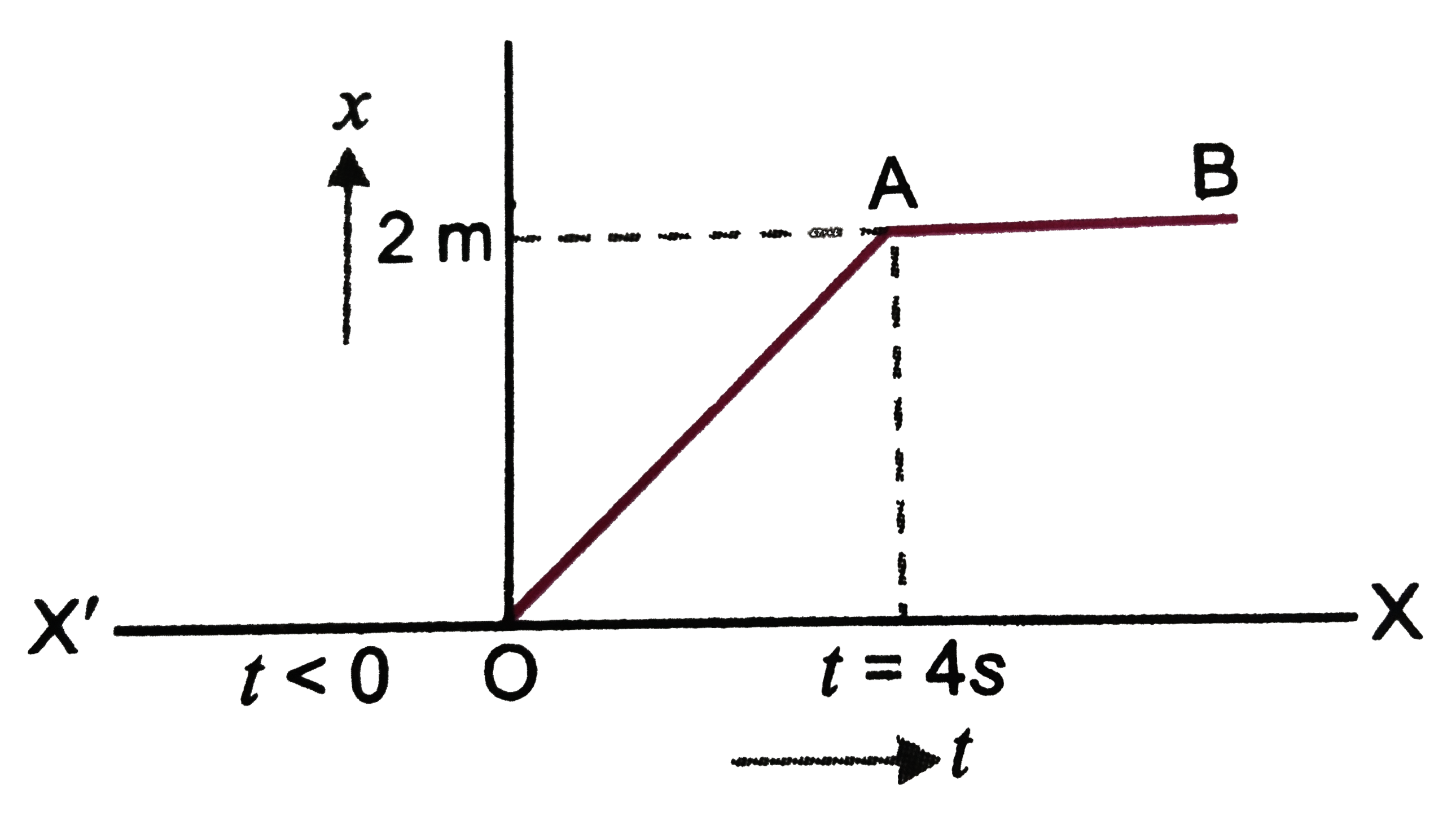 .
.
View Solution

