The length of a rectangular banner is 3 feet 2 inches, and the width is 2 feet 4 inches. Which one of the following equals the area of the banner?
5 sq. feet
5 1/2 sq. feet
6 1/3 sq. feet
7 7/18 sq. feet
The correct Answer is:D
To find the area of the rectangular banner, we will first convert the dimensions from feet and inches to feet only, then calculate the area using the formula for the area of a rectangle.
1. Convert Length from Feet and Inches to Feet:
- The length of the banner is given as 3 feet 2 inches.
- We know that 1 foot = 12 inches. To convert inches to feet, we divide the number of inches by 12.
- Convert 2 inches to feet:
2 inches=212 feet=16 feet
- Now, add this to the feet:
Length=3 feet+16 feet=186+16=196 feet
2. Convert Width from Feet and Inches to Feet:
- The width of the banner is given as 2 feet 4 inches.
- Convert 4 inches to feet:
4 inches=412 feet=13 feet
- Now, add this to the feet:
Width=2 feet+13 feet=63+13=73 feet
3. Calculate the Area of the Rectangle:
- The area A of a rectangle is given by the formula:
A=Length×Width
- Substitute the values we found:
A=(196 feet)×(73 feet)
- Multiply the fractions:
A=19×76×3=13318 square feet
4. Convert the Area to Mixed Number:
- To convert 13318 to a mixed number:
- Divide 133 by 18:
133÷18=7(whole number part)
- Calculate the remainder:
133−(18×7)=133−126=7
- Thus, the area can be expressed as:
A=7718 square feet
Final Answer:
The area of the banner is 7718 square feet.
---
- The length of the banner is given as 3 feet 2 inches.
- We know that 1 foot = 12 inches. To convert inches to feet, we divide the number of inches by 12.
- Convert 2 inches to feet:
2 inches=212 feet=16 feet
- Now, add this to the feet:
Length=3 feet+16 feet=186+16=196 feet
- The width of the banner is given as 2 feet 4 inches.
- Convert 4 inches to feet:
4 inches=412 feet=13 feet
- Now, add this to the feet:
Width=2 feet+13 feet=63+13=73 feet
- The area A of a rectangle is given by the formula:
A=Length×Width
- Substitute the values we found:
A=(196 feet)×(73 feet)
- Multiply the fractions:
A=19×76×3=13318 square feet
- To convert 13318 to a mixed number:
- Divide 133 by 18:
133÷18=7(whole number part)
- Calculate the remainder:
133−(18×7)=133−126=7
- Thus, the area can be expressed as:
A=7718 square feet
The area of the banner is 7718 square feet.
Similar Questions
Knowledge Check
- Question 1 - Select One
The width of a rectangular dance floor is w feet. The length of the floor is 6 feet longer than its width. Which of the following expresses the perimeter, in feet, of the dance floor in terms of w ?
A2w + 6B4w + 12Cw2+6Dw2+6w - Question 2 - Select One
Consider all rectangles such that the rectangle's length is greater than the rectangle's width and the length and width are whole numbers of inches. Which of the following perimeters, in inches, is NOT possible for such a rectangle with an area of 144 square inches?
A48B60C80D102 - Question 3 - Select One
The length of a rectangle is three feet less than twice its width. If x represents the width of the rectangle, in feet, which inequality represents the area of the rectangle that is at most 30 square feet?
Ax(2x−3)≤30Bx(2x−3)≥30Cx(3−2x)≤30Dx(3-2x)ge30'
Two friends need a triangular chart paper for a project. They buy a rectangular chart paper of length 30 inches and breadth 20 inches. They cut is across the diagonal and keep one piece each for their respective projects. Find the area of each friend's chart paper.
View Solution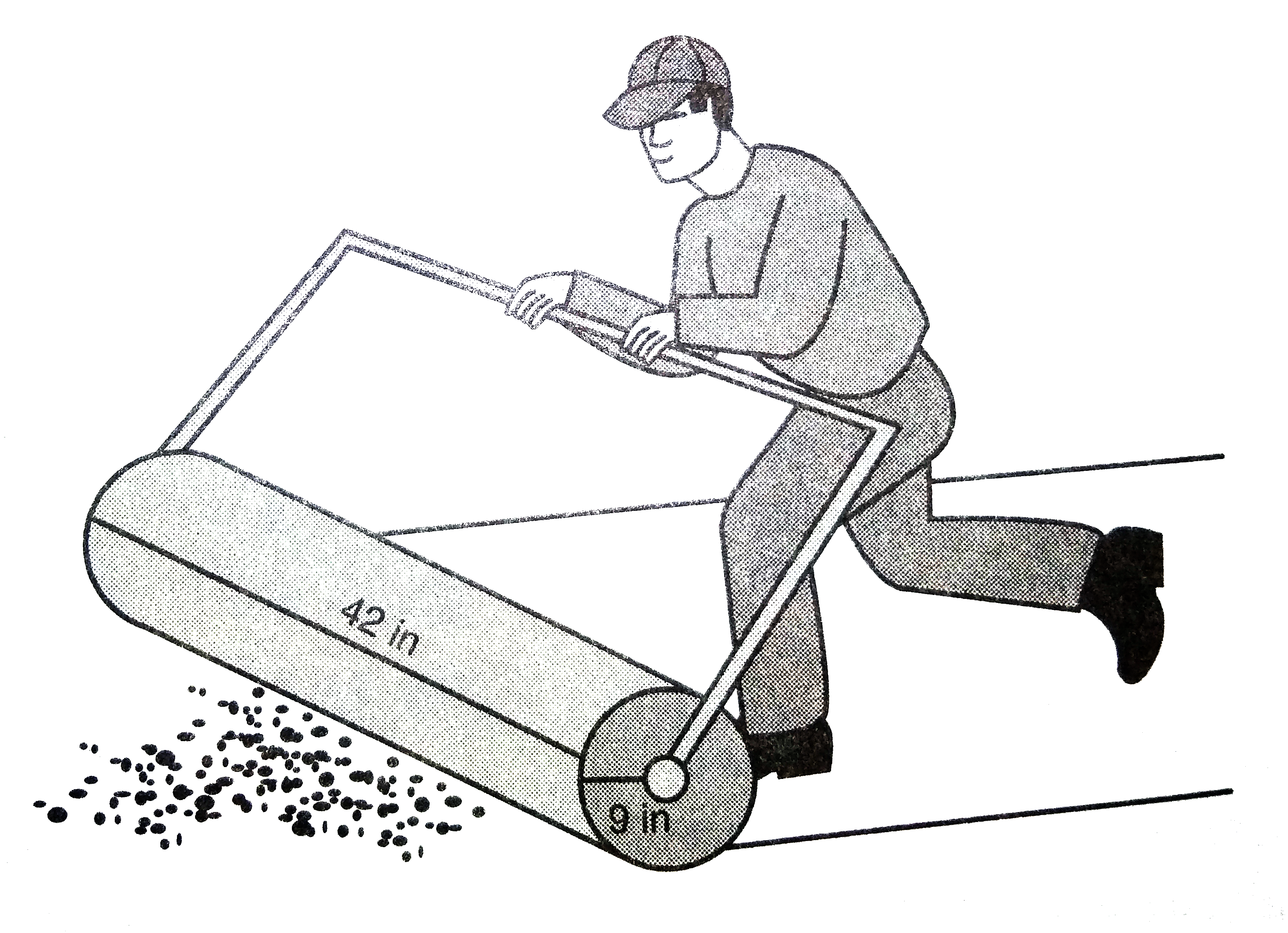
As shown in the figure above, a worker uses a cylindrical roller to help pave a road. The roller has a radius of 9 inches and a width of 42 inches. To the nearest square inch, what is the area of the roller covers in one complete rotation?View SolutionThe area of a rectangular graden is 448 square feet. A statue with a rectangular base that is twice as long as it is wide is placed in the center of the garden so that the garden extends 6 feet beyond the base of the status on the top and bottom and 4 feet beyond the base of the status on the left and right sides. How many feet wide is the base of the status?
View SolutionThe top surface of a rectangular table has an area of 100 square feet and a width of 5 feet. What is the length, in feet, of the surface?
View Solution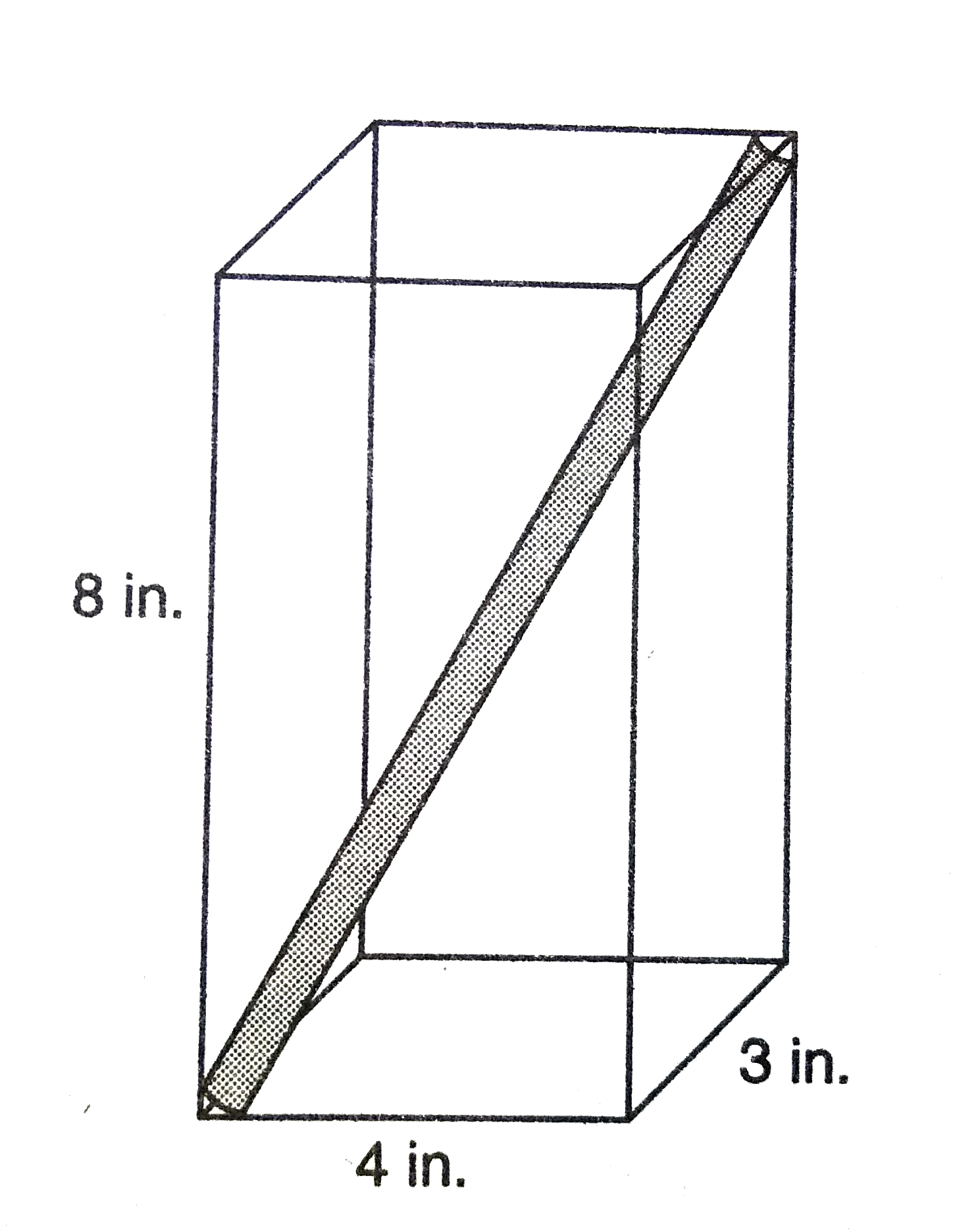
A cylindrical tube with ngligible thichness is placed into a rectangular box that is 3 inches by 4 inches by 8 inches, as shown in the accompanying diagram. If the tubes fits exactly into the box diagonally from the bottom left corner to the top right back corner, what is the best approximately of the number of inches in the length of the cube?View Solution

