Determine which of the two expressions below is larger, whether they are equal, or whether there is not enough information to decide. [The answer is A if Column A is larger, B is Column B is larger ,C if the Columns are equal and D if there is not enough information to decide]
x≠0
Column A −→ x
Column B −→ x2
If column A is larger
If column B is larger
If the columns are equal
If there is not enough information to decide
The correct Answer is:D
To determine which of the two expressions is larger, we will analyze the values of x in both columns. We have:
- Column A: x
- Column B: x2
Given that x≠0, we can consider different cases for x: positive values, negative values, and fractions.
Step 1: Analyze for positive values of x
Let’s first consider when x is positive.
- If x=1:
- Column A: x=1
- Column B: x2=12=1
- Conclusion: Column A = Column B
- If x=2:
- Column A: x=2
- Column B: x2=22=4
- Conclusion: Column B > Column A
Step 2: Analyze for negative values of x
Next, let’s consider when x is negative.
- If x=−1:
- Column A: x=−1
- Column B: x2=(−1)2=1
- Conclusion: Column B > Column A
Step 3: Analyze for fractional positive values of x
Now, let’s consider when x is a positive fraction.
- If x=12:
- Column A: x=12
- Column B: x2=(12)2=14
- Conclusion: Column A > Column B
Summary of Findings
From our analysis, we have:
- For x=1: Column A = Column B
- For x=2: Column B > Column A
- For x=−1: Column B > Column A
- For x=12: Column A > Column B
Final Conclusion
Since the relationship between Column A and Column B changes depending on the value of x, we conclude that there is not enough information to decide which column is consistently larger.
Final Answer: D (There is not enough information to decide)
---
- Column B: x2
- Column A: x=1
- Column B: x2=12=1
- Conclusion: Column A = Column B
- Column A: x=2
- Column B: x2=22=4
- Conclusion: Column B > Column A
- Column A: x=−1
- Column B: x2=(−1)2=1
- Conclusion: Column B > Column A
- Column A: x=12
- Column B: x2=(12)2=14
- Conclusion: Column A > Column B
- For x=2: Column B > Column A
- For x=−1: Column B > Column A
- For x=12: Column A > Column B
Similar Questions
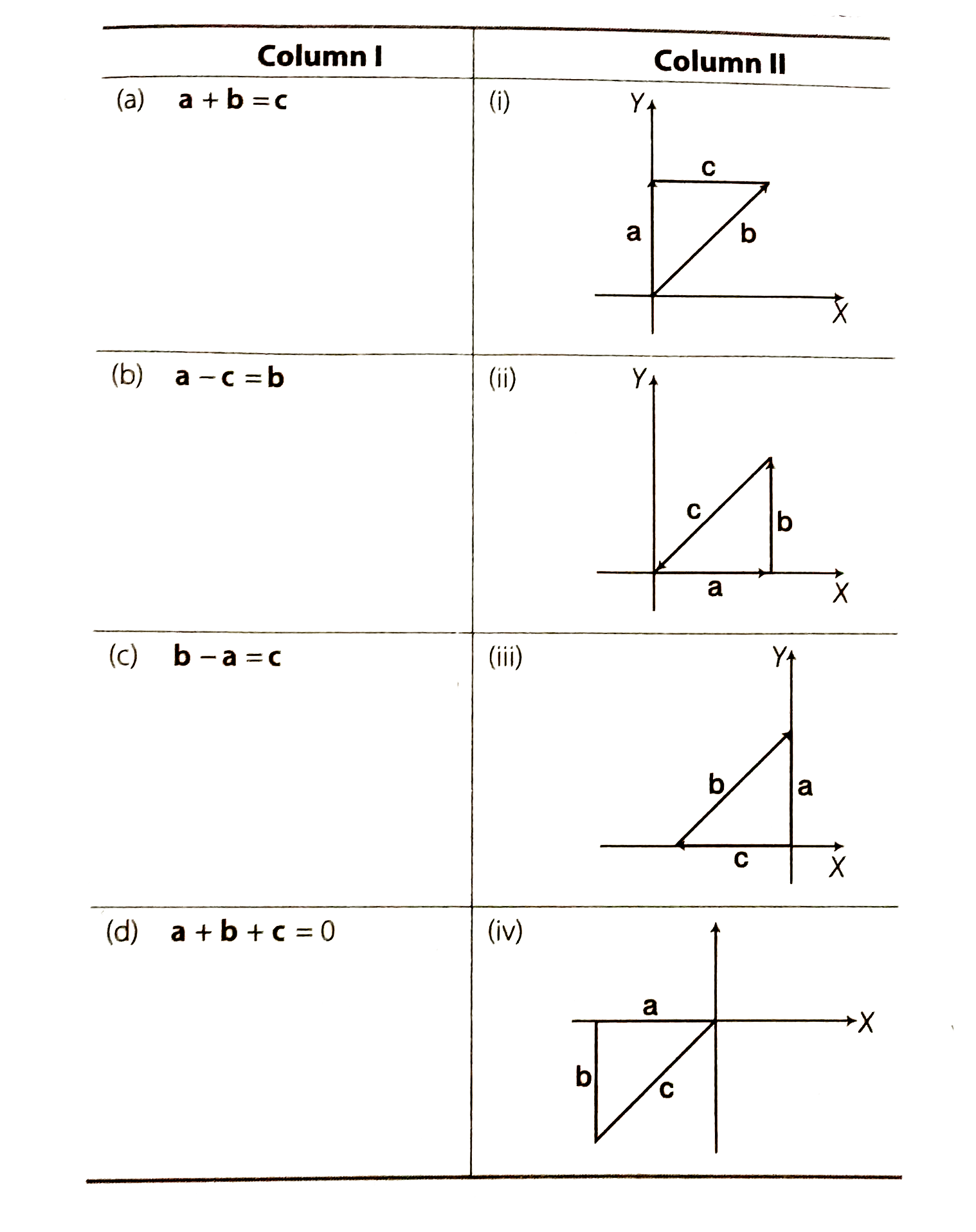
Given below in Column I are the relations between vectors a,b and c and in Column II are the orientations of a, b and c in the XY - plane . Match the relation in Column I to correct orientations in Column II.
View SolutionIf (AB)=BA, where A and B are not square matrices, then number of rows in A is equal to number of columns in B and number of columns in A is equal to number of rows in B.
View Solution
Knowledge Check
Column Ax+y=1Column Bxy
AIf column A is largerBIf column B is largerCIf the columns are equalDIf there is not enough information to decideColumn A0<x<1Column Bx2x
AIf column A is largerBIf column B is largerCIf the columns are equalDIf there is not enough information to decideColumn Ax>0Column B1/2x2x
AIf column A is largerBIf column B is largerCIf the columns are equalDIf there is not enough information to decide
Column Aa2+7a<0ColumnBa0
View SolutionColumn A3x+7y>7x+3yColumnBx+2yy+2x
View SolutionColumn Ax is a two digit number. The digits of the number differ by 6, and the squares of the digits differ by 60Column Bx60
View SolutionLet < x > denote the greatest integer less than or equal to x. For example : <5.5>=5 and <3>=3. Now, which column below is larger?
Column Ax≥0ColumnB√xx
View SolutionColumn A Column BThe first number larger than 300 that is a multiple of both 6 and 8324
View Solution
