In the xy plane, line k has equation y=29x+5, and line n has equation y=14x+b. If the lines intersect at the point with coordinates (a,23) , what is the value of b ?
The correct Answer is:5.54
To find the value of b where the lines intersect at the point (a,23), we will follow these steps:
Step 1: Substitute the intersection point into line k's equation
The equation of line k is given by:
y=29x+5
Since the lines intersect at the point (a,23), we can substitute y=23 into line k's equation:
23=29a+5
Step 2: Solve for a
To solve for a, we first isolate a:
1. Subtract 5 from both sides:
23−5=29a
2. Convert 5 to a fraction with a denominator of 3:
5=153
Thus,
23−153=29a
This simplifies to:
−133=29a
3. Multiply both sides by 92 to solve for a:
a=−133⋅92=−1176=−392
Step 3: Substitute a into line n's equation
The equation of line n is:
y=14x+b
Substituting a=−392 and y=23:
23=14(−392)+b
Step 4: Solve for b
1. Calculate 14(−392):
14⋅−392=−398
2. Substitute back into the equation:
23=−398+b
3. Isolate b:
b=23+398
4. Convert 23 to a fraction with a denominator of 24:
23=1624
5. Convert 398 to a fraction with a denominator of 24:
398=11724
6. Now add the two fractions:
b=1624+11724=13324
Final Answer
Thus, the value of b is:
b=13324
The equation of line k is given by:
y=29x+5
Since the lines intersect at the point (a,23), we can substitute y=23 into line k's equation:
23=29a+5
To solve for a, we first isolate a:
1. Subtract 5 from both sides:
23−5=29a
2. Convert 5 to a fraction with a denominator of 3:
5=153
Thus,
23−153=29a
This simplifies to:
−133=29a
3. Multiply both sides by 92 to solve for a:
a=−133⋅92=−1176=−392
The equation of line n is:
y=14x+b
Substituting a=−392 and y=23:
23=14(−392)+b
1. Calculate 14(−392):
14⋅−392=−398
2. Substitute back into the equation:
23=−398+b
3. Isolate b:
b=23+398
4. Convert 23 to a fraction with a denominator of 24:
23=1624
5. Convert 398 to a fraction with a denominator of 24:
398=11724
6. Now add the two fractions:
b=1624+11724=13324
Thus, the value of b is:
b=13324
Similar Questions
Knowledge Check
In the xy-plane, the point (p, r) lies on the line with equation y = x + b, where b is a constant. The point with coordinates (2p, 5r) lies on the line with equation y = 2x + b. If p ≠ 0, what is the value of rp ?
A25B34C43D52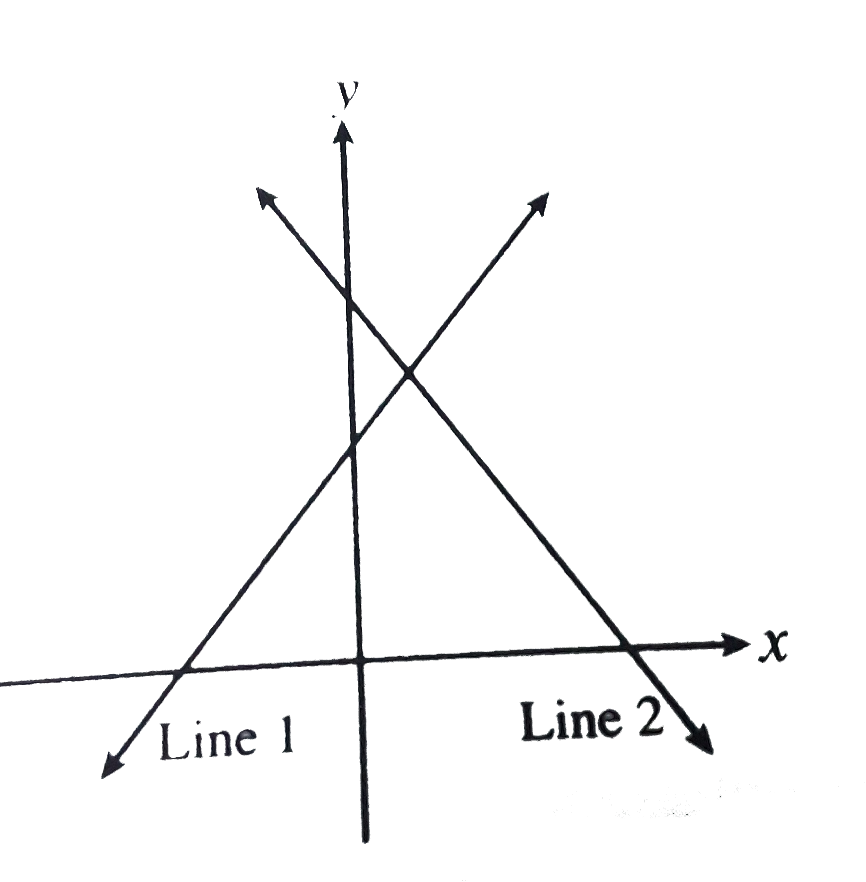
Consider two lines in the xy-plane , as shown above. If line 1 has equation y=m1x+b1, and line 2 has equation y=m2x+b2. Which is a true statement ?Am1<m2Bb1<b2Cb2<0Dm2>0
In the xy-plane , a line that has the equation y=c for some constant c intersects a parabola at exactly one point. If the parabola has the equation y=−x2+5x, what is the value of c ?
View SolutionThe equation of a circle in the xy-plane is x2+4x+y2−10y=20. If the line x=k intersects the circle in exactly one point, what is the possible value of k?
View SolutionA line has the equation x=y80−20. At which point will this line intersect the x - axis?
View SolutionA line has the equation x=y80−20. At which point does this line intersect the x-axis?
View SolutionThe line represented by the equation y=−2x+6 is the perpendicular bisector of the line segment AB. If A has the coordinates (7,2), what are the coordinates for B?
View SolutionIn the xy-plane, line l has a y-intercept of −13 and is perpendicular to the line with equationy= − 23 x. If the point (10, b) is on line l, what is the value of b ?
View Solution
