A 7-foot ladder is leaning against a wall such that the angle relative to the level ground is 70∘. Which of the following expressions involving cosine gives the distance, in feet, from the base of the ladder to the wall?
7cos70∘
cos70∘7
17cos7∘
7cos70∘
The correct Answer is:D
To solve the problem of finding the distance from the base of the ladder to the wall, we can use trigonometric relationships in a right triangle. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have a right triangle formed by the wall, the ground, and the ladder. The ladder is the hypotenuse, the distance from the base of the ladder to the wall is the base, and the height of the ladder against the wall is the perpendicular.
Step 2: Identify the Given Information
- Length of the ladder (hypotenuse, AC) = 7 feet
- Angle with the ground (∠CAB) = 70 degrees
Step 3: Use the Cosine Function
In a right triangle, the cosine of an angle is defined as the ratio of the length of the adjacent side (base) to the length of the hypotenuse. Thus, we can write:
cos(70∘)=Base (AB)Hypotenuse (AC)
Step 4: Substitute the Known Values
Substituting the known values into the equation:
cos(70∘)=AB7
Step 5: Solve for the Base (AB)
To find the distance from the base of the ladder to the wall (AB), we can rearrange the equation:
AB=7⋅cos(70∘)
Conclusion
Thus, the expression that gives the distance from the base of the ladder to the wall is:
AB=7cos(70∘)
The correct answer is option D: 7cos(70∘).
---
We have a right triangle formed by the wall, the ground, and the ladder. The ladder is the hypotenuse, the distance from the base of the ladder to the wall is the base, and the height of the ladder against the wall is the perpendicular.
- Length of the ladder (hypotenuse, AC) = 7 feet
- Angle with the ground (∠CAB) = 70 degrees
In a right triangle, the cosine of an angle is defined as the ratio of the length of the adjacent side (base) to the length of the hypotenuse. Thus, we can write:
Substituting the known values into the equation:
To find the distance from the base of the ladder to the wall (AB), we can rearrange the equation:
Thus, the expression that gives the distance from the base of the ladder to the wall is:
Similar Questions
A 13 m long ladder is leaning against a wall, touching the wall at a certain height from the ground level. The bottom of the ladder is pulled away from the wall, along the ground, at the rate of 2 m/s. How fast is the height on the wall decreasing when the foot of the ladder is 5 m away from the wall ?
View SolutionA ladder 13 m long is leaning against a wall. The bottom of the ladder is pulled along the ground away from the wall at the rate of 4 m/sec. Find the rate of decreasing at which the top of the ladder moving downwards on wall when the foot of the ladder is 5 m away from the wall.
View Solution
Knowledge Check
As shown in the figure below , a skatebond ramp leading from the top of a boulder is 10 feet long and forms a 32∘ angle with the level ground . Which of the following expressions represents the height, in the feet , of the boulder ?
 A10tan32∘Bsin32∘10C10cos32∘D10sin32∘
A10tan32∘Bsin32∘10C10cos32∘D10sin32∘The bottom of the basket of a hot-air balloon is parallel to the level ground. One taut tether line 144 feet long is attached to the centre of the bottom of the basket and is anchored to the ground at an angle of 72∘, as shown in the figure below. Which of the following expressions gives the distance, in feet, from the center of the bottom of the basket to the ground?
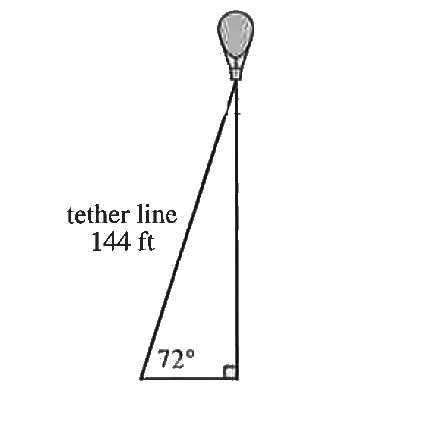 A144cos72∘B144sin72∘C144tan72∘D144sin72∘
A144cos72∘B144sin72∘C144tan72∘D144sin72∘As shown above, a 10 - foot ramp forms an angle of 23∘ with the ground, which is horizontal. Which of the following is an expression for the vertical rise, in feet, of the ramp?
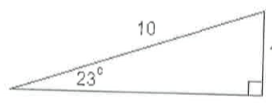 A10cos23∘B10sin23∘C10tan23∘D10cot23∘
A10cos23∘B10sin23∘C10tan23∘D10cot23∘
A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall?
View SolutionA ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall?
View SolutionA 6.5 m long ladder is placed against a wall such that its foot is at a distance of 2.5 m from the wall. Find the height of the wall where the top of the ladder touches it
View SolutionA ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder.
View SolutionA ladder rests against the side of a wall and reaches a point that is h meters above the ground. The angle formed by the ladder and the ground is θ∘. A point on the ladder is k meters from the wall.What is the vertical distance, in meters, from this point on the ladder to the ground?
View Solution
