Tickets for a concert cost for children and for adults. 850 concert tickets were sold for a total cost of . How many children's tickets were sold?
The correct Answer is:640
To solve the problem, we will set up a system of equations based on the information given about the concert tickets.
Step 1: Define Variables
Let:
- x = number of children's tickets sold
- y = number of adult tickets sold
Step 2: Set Up the Equations
From the problem, we know:
1. The total number of tickets sold (children's + adults) is 850:
x+y=850(Equation 1)
2. The total revenue from the tickets sold is $3820. Since children's tickets cost $4 and adult tickets cost $6, we can express this as:
4x+6y=3820(Equation 2)
Step 3: Solve Equation 1 for y
From Equation 1, we can express y in terms of x:
y=850−x(Equation 3)
Step 4: Substitute Equation 3 into Equation 2
Now, substitute Equation 3 into Equation 2:
4x+6(850−x)=3820
Expanding this gives:
4x+5100−6x=3820
Step 5: Combine Like Terms
Combine the x terms:
−2x+5100=3820
Step 6: Isolate x
Subtract 5100 from both sides:
−2x=3820−5100
−2x=−1280
Now, divide by -2:
x=12802=640
Step 7: Find y
Now that we have x, we can find y using Equation 3:
y=850−640=210
Conclusion
The number of children's tickets sold is 640.
Let:
- x = number of children's tickets sold
- y = number of adult tickets sold
From the problem, we know:
1. The total number of tickets sold (children's + adults) is 850:
x+y=850(Equation 1)
4x+6y=3820(Equation 2)
From Equation 1, we can express y in terms of x:
y=850−x(Equation 3)
Now, substitute Equation 3 into Equation 2:
4x+6(850−x)=3820
Expanding this gives:
4x+5100−6x=3820
Combine the x terms:
−2x+5100=3820
Subtract 5100 from both sides:
−2x=3820−5100
−2x=−1280
Now, divide by -2:
x=12802=640
Now that we have x, we can find y using Equation 3:
y=850−640=210
The number of children's tickets sold is 640.
Similar Questions
Knowledge Check
Tickets for a concert cost $4.50 for children and $12.00 for adults. 4460 concert tickets were sold for a total cost of $29,220. Solving which of the following systems of equations yeilds the number of children, c, and numbr of adults, a, that purchased concert tickets?
Ac+a=4460
4.50+12a=58.440Bc+a=4460
4.50c+12a=29,220Cc+a=4460
4.50c+12a=14,610Dc+a=29,220
4.50c+12a=4460Ticket prices for a school play are $7.50 for students and $10.00 for adults . For a given performance , 200 tickets were sold , and the performance took in $1,775. Solving which of the following systems of equations yields the number of student tickets , x , and the number of adult ticket , y, that were bought for that performance ?
Ax+y=200
7.5x+10y=1,775Bx+y=1,775
7.5x+10y=200Cx+y=200
7.5x+10y=1,7752Dx+y=1,775
7.5x+10y=(1,775)(2)Tickets to the annual Follies Show at Littleton High School are $4 for adults and $2.50 for students. There is a cost of $750 to produce the show. If the x-axis represents the number of adult tickets sold and the y-axis represents the number of student tickets sold, which graph represents all the possible combinations of ticket sales that allow the junior class to at least cover the cost of the show ?
A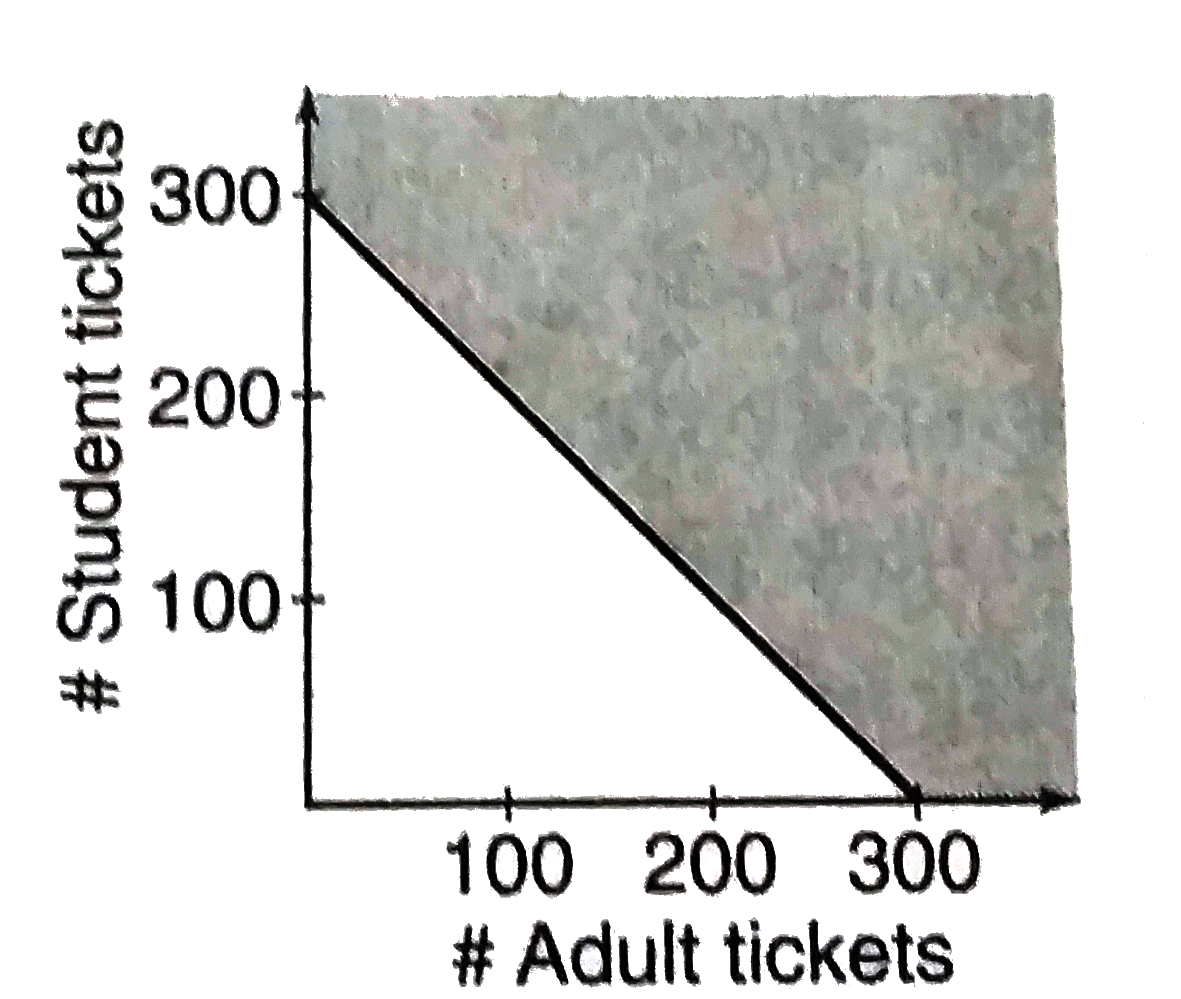 B
B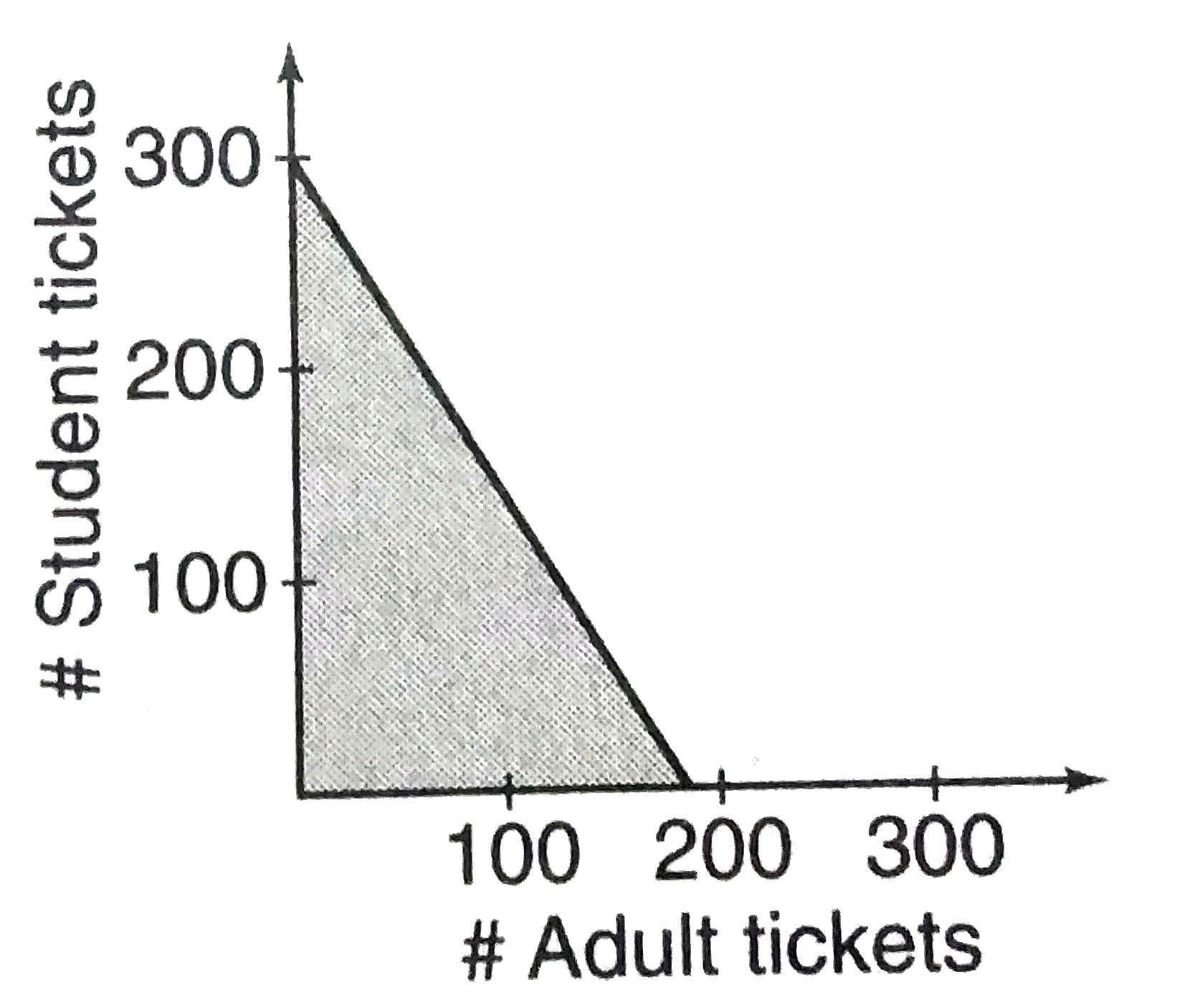 C
C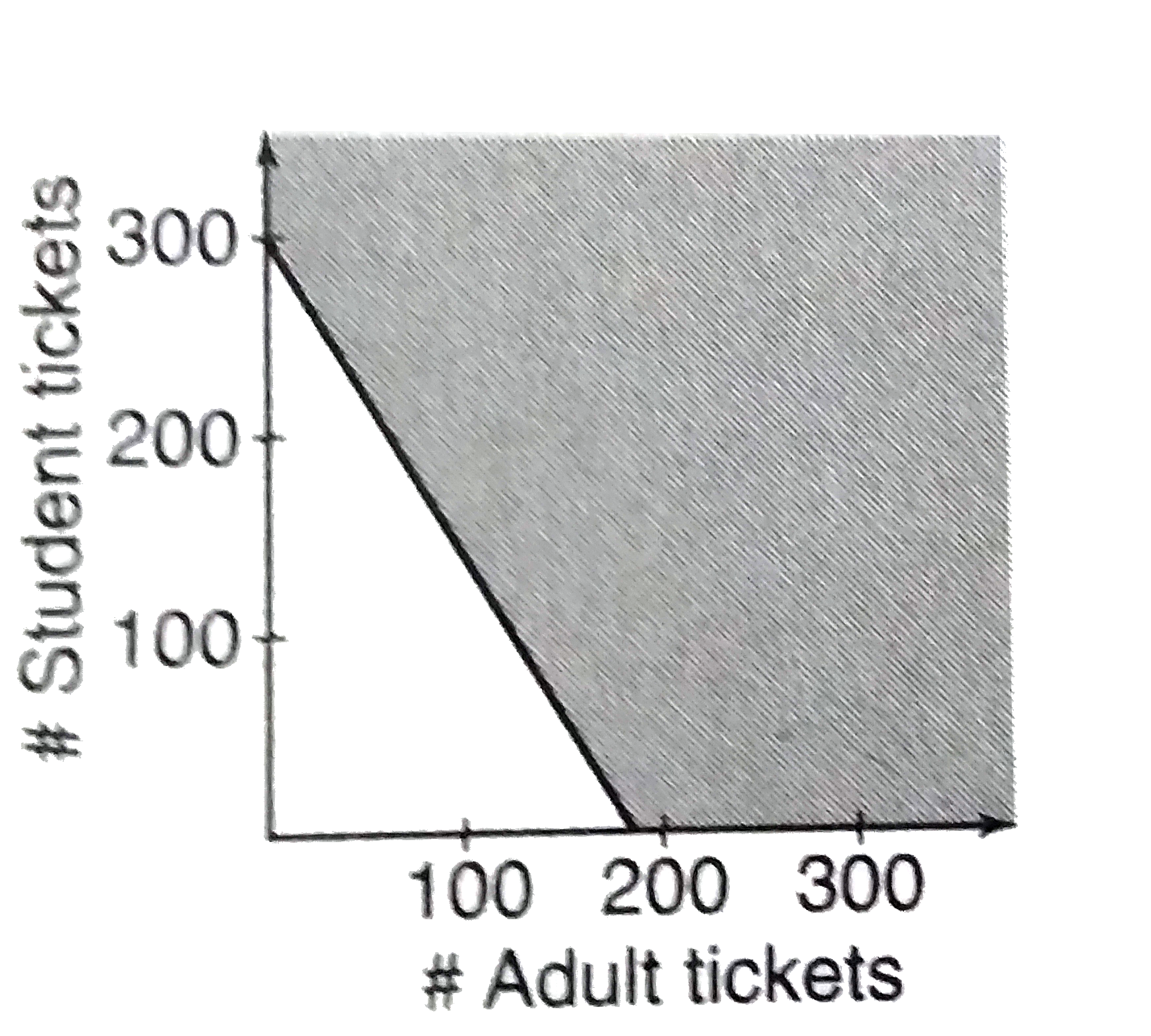 D
D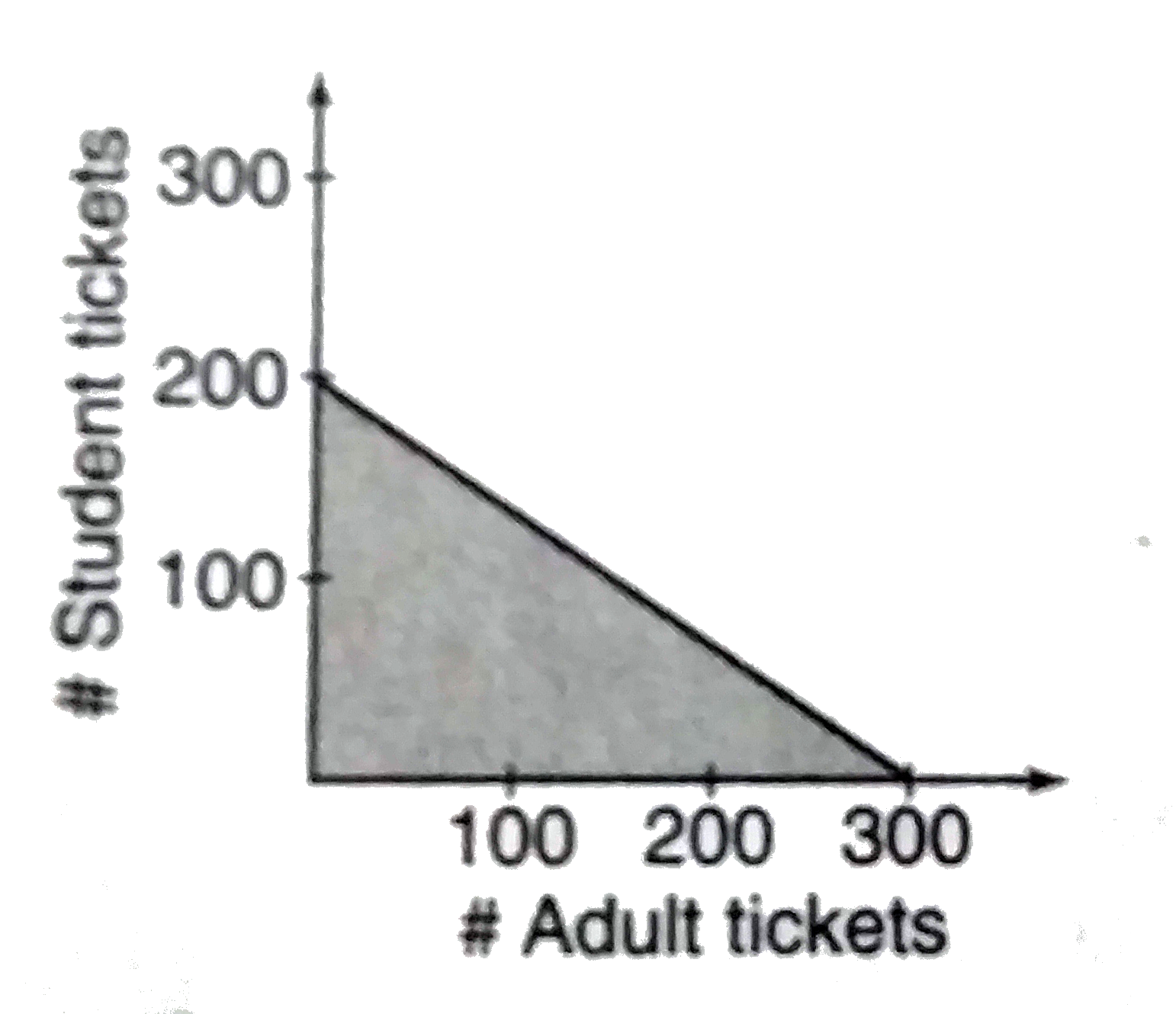
Tickets for a school talent show cost $2 for students and $3 for adults. If Chris spends at least $11 but no more than $14 on x student tickets and 1 adult ticket, what is one possible value of x ?
View SolutionIn a charity show Rs 6496 were collected by selling some tickets. If the price of each ticket was Rs 5034, how many tickets were sold?
View SolutionA store sells shirts fro $7.50 each and hats for $5.00 each. The store earns $1,822.50 in one day from selling a total of 307 shirts and hats. How many shirts were sold on that day?
View SolutionA gas station sells regular gasoline for $2.39 per gallon and premium gasoline for $2.79 per gallon. If the gas station sold a total of 550 gallons of both types of gasoline in one day for a total of $1.344.50. how many gallons of premium gasoline were sold?
View SolutionTwo types of tickets were sold for a concert held at an amphitheater. Tickets to sit on a bench during the concert cost $75 each, and tickets to sit on the lawn during the concert cost $40 each. Organizers of the concert announced that 350 tickets had been sold and that $19,250 had been raised through ticket sales alone. Which of the following systems of equations could be used to find the number of tickets for bench seats, B, and the number of tickets for lawn seats, L, that were sold for the concert?
View Solution


