Question

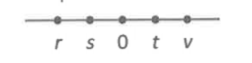
On the number line, the distance between the point whose coordinate is s and the point whose coordinate is t is greater than 500. Which of the following must be true?
I. $\left|s\right|.\left|t\right|>500$
II. $|s-t|>500$
III. $t-s>500$

Options

A. I only
B. II only
C. I and II only
D. I, II, and III

Answer

B

Explanation

To solve the problem, we need to analyze the given statements based on the condition that the distance between the points $$s$$ and $$t$$ on the number line is greater than 500.

1. Understanding the Distance Condition:
The distance between two points \( s \) and \( t \) on a number line is given by the absolute value of their difference:
\( |s - t| > 500 \)
This means that the distance between \( s \) and \( t \) must be greater than 500.

2. Analyzing the Statements:
Now, let's evaluate each of the statements provided:

Statement I: \( |s| \cdot |t| > 500 \)
- This statement is not necessarily true. For example, if \( s = 1 \) and \( t = 600 \), then \( |s| \cdot |t| = 1 \cdot 600 = 600 > 500 \) holds true. However, if \( s = 0 \) and \( t = 600 \), then \( |s| \cdot |t| = 0 \cdot 600 = 0 \), which does not satisfy the condition. Thus, Statement I is not necessarily true.

Statement II: \( |s - t| > 500 \)
- This statement is directly derived from the distance condition we established. Since it is given that the distance between \( s \) and \( t \) is greater than 500, this statement is true.

Statement III: \( t - s > 500 \)
- This statement assumes a specific order of \( s \) and \( t \). If \( s < t \), then \( t - s > 500 \) would be true. However, if \( s > t \), then \( s - t > 500 \) would hold instead. Therefore, Statement III is not necessarily true as it does not account for both scenarios.

3. Conclusion:
Based on the evaluations:
- Statement I is not necessarily true.
- Statement II is true.
- Statement III is not necessarily true.

Thus, the only statement that must be true is Statement II.

Final Answer:
The answer is II only.

---