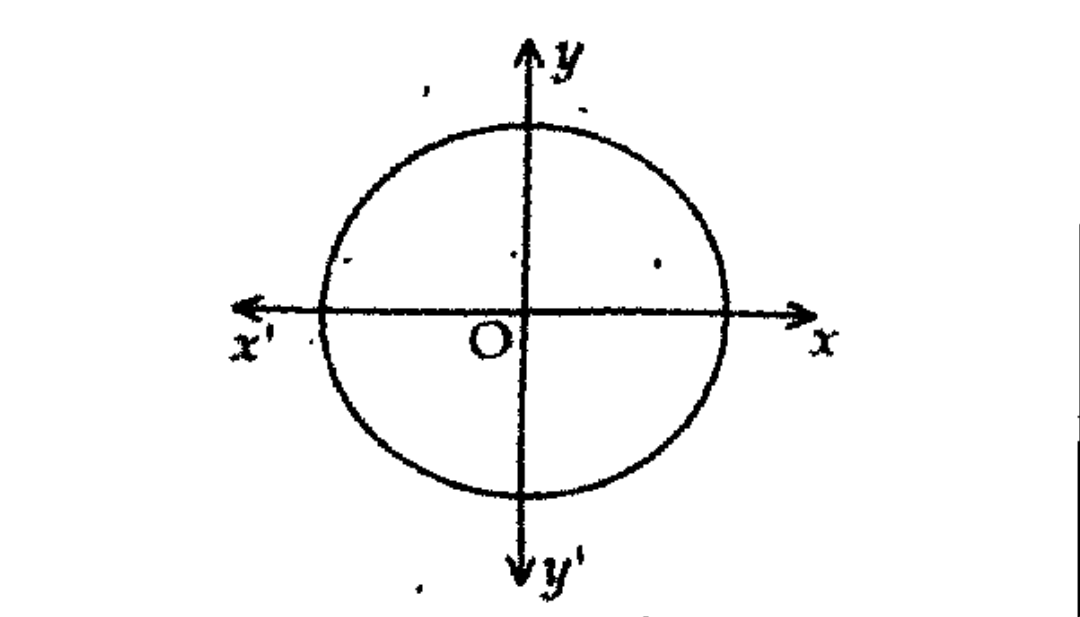
The equatinn of the circle with centre origin and radius 2 isSolution in Telugu
x2+y2−6x+4y+4=0
x2+y2=4
x2+y2−4x+6y−12=0
x2+y2+2x+16y+40=0
The correct Answer is:B
Step by step video, text & image solution for The equatinn of the circle with centre origin and radius 2 is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - CIRCLEEXERCISE - Exercise 1B(Circle-Line)142videos
CIRCLE
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - CIRCLEEXERCISE - Exercise 1C(Pole, Polar)107videos
CIRCLE
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - CIRCLEEXERCISE - Set 44videos
CIRCLE
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - BINOMIAL THEOREMEXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) SET - 44videos
BINOMIAL THEOREM
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - COMPLEX NUMBERS EXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) (SET - 4)5videos
COMPLEX NUMBERS
Similar Questions
The equation of the tangent to the cirele x2+y2−2x−4y+3=0 at (2,3)is
04:27View SolutionThe polar of the point (3,4) w.r.t. x2+y2=25 is
02:04View SolutionA: The equation of the circle (2,-3), (-3,2) as ends of a diameter is x2+y2+x+y−12=0
R: The equation of the circle having the line segment joining A(x1,y1)andB(x2,y2) as diameter (x−x1)(x−x2)+(y−y1)(y−y2)=003:07View SolutionA : If the coefficients of 5th, 6th , 7th terms of (1+x)n are in A.P. then n=7or14.
R : If the coefficients of rth, (r+1)th,(r+2)th terms of (1+x)n are in A.P. then n2−(4r+1)n+4r2=2.02:43View SolutionA : If argument of z1=π/3 , argument of z2=π/4 then argument of z1z2 is 7π/12
R : Arg (z1z2)=Argz1+Argz202:14View SolutionIf the length of the normal for each point on a curve is equal to the radius vector,then the curve (a) is a circle passing through origin (b) is a circle having centre at origin and radius 0 (c) is a circle having centre on x-axis and touching y-axis (iv) is a circle having centre on y-axis and touching x-axis
04:19View SolutionA circle is draw with origin as centre and passing through ( 2 , 3) , then its radius is ...
View SolutionEquation of circle of radius 5, centred on X -axis and
passing through origin , is03:01View SolutionEquation of circle throught origin, having radius 5 and abscissa of centre is (-3) .
00:56View SolutionEquation of the circle with centre on the X-axis , radius 4 , and passing through the origin , is
02:34View SolutionA circle has its centre on the y-axis and passes through the origin, touches anotgher circle with centre (2,2) and radius 2, then the radius of the circle is
03:05View SolutionC1 is a circle with centre at the origin and radius equal to r and C2 is a circle with centre at (3r, 0) and radius t 2r. The number of common tangents that can be drawn to the two circles are
04:28View SolutionTwo circles of equal radius of 5 units have their centres at the origin and the point (2,−3). Equation of the common chord of these circles is
View SolutionObtain equation of circle in Centre of origin and radius r = 6.
02:09View SolutionIn the figure, O is the centre of the circle and x2+y2=25 is the equation of the circle.
Write the equation of the circle whose centre is at the origin and radius is 3.
 .01:16View Solution
.01:16View Solution


