A random variable X has the probability distribution:
X:12345678p(X):0.150.230.120.100.200.080.070.05
For the events E={X is a prime number} and F={X<4}, the probability P(E∪F) is Solution in Telugu
0.87
0.5
0.35
0.77
The correct Answer is:D
Step by step video, text & image solution for A random variable X has the probability distribution: {:(X:,1,2,3,4,5,6,7,8),(p(X):,0.15,0.23,0.12,0.10,0.20,0.08,0.07,0.05):} For the events E={X is a prime number} and F={X lt 4}, the probability P(E uu F) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - THEORETICAL DISTRIBUTIONSEXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) CHOOSE THE CORRECT ANSWER FROM THE ALTERNATIVES 1.2.3 OR 4 GIVEN (SET -1)4videos
THEORETICAL DISTRIBUTIONS
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - THEORETICAL DISTRIBUTIONSEXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) CHOOSE THE CORRECT ANSWER FROM THE ALTERNATIVES 1.2.3 OR 4 GIVEN (SET -2)3videos
THEORETICAL DISTRIBUTIONS
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - THEORETICAL DISTRIBUTIONSEXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) CHOOSE THE CORRECT ANSWER FROM THE ALTERNATIVES 1.2.3 OR 4 GIVEN (SET -4)5videos
THEORETICAL DISTRIBUTIONS
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - THE PLANEEXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) SET 44videos
THE PLANE
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - THEORY OF EQUATIONSEXERCISE - SET - 44videos
THEORY OF EQUATIONS
Similar Questions
A random variable X follows the following distribution
(X=xi:,0,1,2,3),(P(X=xi):,2/6,3/6,0/6,1/6,)
The mean and the variance are01:46View SolutionA random avriable X has its range {1,2,3}. P(X=1)=1/6,P(X=2)=1/3,P(X=3)=1/2. If mean =a, variance =b and standard =c then the descending order of a,b,c, is
03:49View SolutionA: A random variable X has the range {1,2,3}. If P(X=1)=c, P(X=2)=3c,P(X=3)=6c then c=1/10.
R: If :S→R is a discreate random variable with range (x1,x2,x3,…………} then∞∑r=1(X=x)=104:19View SolutionA: The equation of the plane passing through the point (- 1, 2, 4) and parallel to the plane 2x + 3y – 5z +6=0 is 2x + 3y - 5z + 16 = 0.
R: The equation of the plane passing through the point (x1,y1,z1) and parallel to the plane ax + by + cz +d=0 is a(x–x1)+b(y−y1)+c(z−z1)=003:02View SolutionA : the equation whose roots are multiplied by 2 of those of x5−2x4+3x3−2x2+4x+3=0 is x5−4x4+12x3−16x2+64x+96=0.
R: the equation whose roots are multiplied by k of those of f(x) = 0 is f(x/k) = 0.03:35View SolutionA random variable has the following probability distribution: 1 2 3 4 5 6 7 8 For the events E=[X:X is a prime number], F={X:X<4} , the probability P(E∪F) is 0.50 b. 0.77 c. 0.35 d. 0.87
01:33View SolutionA random variable X has the following probability distribution :
X:12345678P(X):0.150.230.120.100.200.080.070.08
for the events E=[X is a prime number] F={X<4}, the probability P(EOP), is.View SolutionA random variable X has the follwing probability distribution:

Find P(0<X<4)03:48View SolutionA random variable X has the following probability distribution:

Then E(X) = …….02:11View SolutionA random variable X has the probability distribution
For the events E = {X is a prime number} abd F={X<4},P(E∪F) is
 02:41View Solution
02:41View Solutionकिसी यदृच्छया चर का प्रायिकता वितरण निम्नवत है :
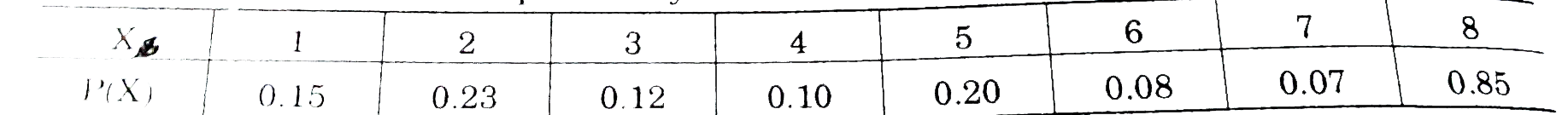
घटना E के लिए = {X एक अभाज्य संख्या है ।} तथा F=(X<4),P(E∪F) कि प्रायिकता है :04:02View Solutionयदि यादृच्छिक चर X के संगत प्रायिकता P(X) हो, तो घटना E का X का माध्य E(X) =…………….होगा।
03:21View SolutionA random varticle X has the probability distribution :
X:12345678P(X):0.150.230.120.100.200.080.070.05
For the events E = {X is a prime number } and F={X<4} , the probability P(E∪F) is :View SolutionA random variable X has the probability distribution:

For the events E = (X is prime number) and F = {X < 4}, the probability P(E∪F) is03:16View SolutionThe probability distribution of a random variable X is as follows - {:(X :,1,2,3,4,5,6,7,8),(p(X) : ,0.15,0.23,0.12,0.10,0.20,0.08,0.07,0.05):} So the event E = {X is a prime number} and F = {X lt 4} Probability for P (C cup F) is -
View Solution

