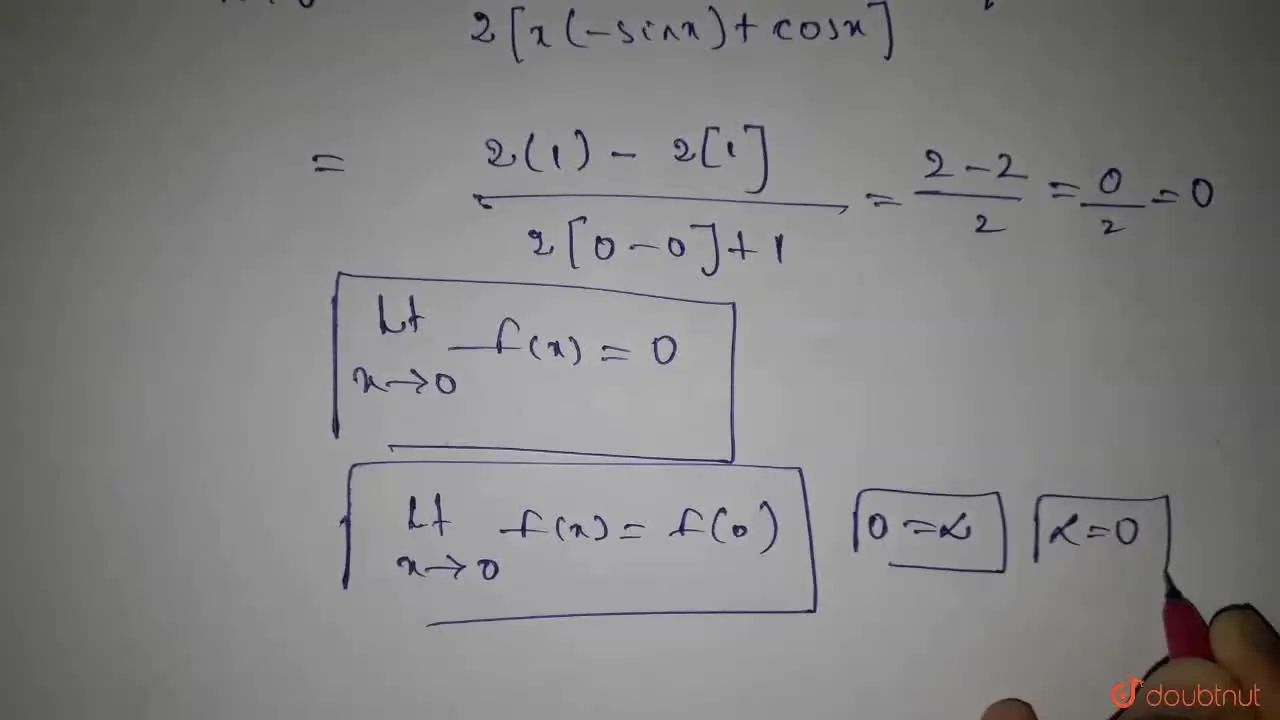If fR→R is defined by f(x)={2sinx−sin2x2xcosx if x≠0α for x=0 then the value of alpha so that f is continuous at 0 is Solution in Telugu
2
1
−1
0
The correct Answer is:D
Step by step video, text & image solution for If f R to R is defined by <by> f (x) = {{:(( 2 sin x - sin 2x)/(2x cos x ) " if " x ne 0) , ( alpha " for " x =0 ):} then the value of alpha so that f is continuous at 0 is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - LIMITS AND CONTINUITYEXERCISE - Exercise 2(Special Type Questions)10videos
LIMITS AND CONTINUITY
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - LIMITS AND CONTINUITYEXERCISE - SET-3Match The Following2videos
LIMITS AND CONTINUITY
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - LIMITS AND CONTINUITYEXERCISE - Exercise 1B( One Sided Limits)71videos
LIMITS AND CONTINUITY
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) (SET - 4)5videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - LINEAR PROGRAMMING [APPENDIX-2]EXERCISE - Exercise -133videos
LINEAR PROGRAMMING [APPENDIX-2]
Similar Questions
I. Ltx→0(1+x)2−(1−x)2−2(1+x)3−(1−x)3−3
II. If f(x)=4−7x3x+4andLtx→2f(x)=l,Ltx→0f(x)=m then the equation whose roots are 1/l, 1/m is x2−1=002:23View SolutionMatch the following
 03:36View Solution
03:36View SolutionLtx→0√x=
03:57View SolutionA : The maximum value of f(x)=Sin−1x+Cos−1x−Tan−1x is 3π/4
R : Sin−1x+Cos−1x=π/2∀x∈RView SolutionIf 2x+y≥10,x+2y≥10, then the lesat value of F=x+y is
04:38View SolutionIf R→R is defined by
f(x)={2sinx−sin2x2xcosx,if x≠0a,if x=0
then the value of a so that f is continuous at x = 0 isView SolutionIf f(x) is a continuous function in [0,π] such that f(0)=f(x)=0, then the value of
∫π/20{f(2x)−f''(2x)}sinxcosxdx is equal to02:22View SolutionIf f(x)=2x+3sinx3x+2sinx,x≠0 is continuous at x = 0 , then find f(0)
03:47View SolutionLet f:R→R is defined by f(x)= {{:(,alpha+(sin [x])/(x),if x gt 0),(,2,if x =0),(,beta+[(sin x-x)/(x^(3))], if x lt 0):}where[y]de¬esthe∫egralpartofy.Iffiscont∈uousatx=0,thenbeta-alpha=
View SolutionThe function f(x)=1−cosax1−cosbxfor x≠0,f(0)=ab at x= 0 is
02:04View SolutionLet F :R→R be defined by
f(x)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩α+sin[x]x if x>02 if x=0β+[sinx−xx3]if x<0
where , [x] denotes the integral part of x. If f continuous at x =0, then β=α is equal to04:19View SolutionIf f: R → R is defined by f(x)={2sinx−sin2x2xcosxifx≠0aifx≠0
then the value of 'a' so that f is continuous at 0 is06:16View SolutionIs f defined by f(x)={sin2xxifx≠01ifx=0 continuous at 0?
01:51View SolutionLet f(x)=sin(πcos2x)x2,x≠0 . The value of f(0) so that f is a continuous function is
02:27View SolutionIf f(x)={sin5x2xx≠0kx=0 is continuous at x = 0 then value of k is :
03:47View Solution