Statement-I : The point A(3,1,6) is the miror image of the point B(1,3,4) in the plane x−y+z=5.
Statement-II : The plane x−y+z=5 bisects the line segment joining A(3,1,6) and B(1,3,4)Solution in Telugu
Statement-1 is true, statement-2 is true, statement-2 is a correct explanation for statement-1
Statement-1 is true, statement-2 is true, statement-2 is not a correct explanation for statement-1
Statement-1 is true, statement-2 is false.
Statement-1 is false, statement-2 is true.
The correct Answer is:B
Step by step video, text & image solution for Statement-I : The point A(3,1,6) is the miror image of the point B(1,3,4) in the plane x-y+z=5. Statement-II : The plane x-y+z=5 bisects the line segment joining A(3,1,6) and B(1,3,4) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THE PLANEBook:DIPTI PUBLICATION ( AP EAMET)Chapter:THE PLANEExercise:EXERCISE 2 (SPECIAL TYPE QUESTIONS) SET 3
Explore 4 Videos
- SYSTEM OF CIRLES Book:DIPTI PUBLICATION ( AP EAMET)Chapter:SYSTEM OF CIRLES Exercise:EXERCISE 2 (SET-4 )
Explore 4 Videos
- THEORETICAL DISTRIBUTIONSBook:DIPTI PUBLICATION ( AP EAMET)Chapter:THEORETICAL DISTRIBUTIONSExercise:EXERCISE 2 (SPECIAL TYPE QUESTIONS) CHOOSE THE CORRECT ANSWER FROM THE ALTERNATIVES 1.2.3 OR 4 GIVEN (SET -4)
Explore 5 Videos
Similar Questions
Match the following
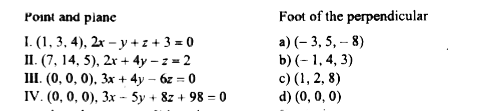
View SolutionA : If x2+y2−2x+3y+k=0,x2+y2+8x06y−7=0 cut each other orthogonally then k = 10 .
R : The circles x2+y2+2gx+2fy+c=0,x2+y2+2g'x+2f'y+c'=0 cut each other orthogonally iff 2gg'+2ff'=c+c'
View SolutionA: A random variable X has the range {1,2,3}. If P(X=1)=c, P(X=2)=3c,P(X=3)=6c then c=1/10.
R: If :S→R is a discreate random variable with range (x1,x2,x3,…………} then∞∑r=1(X=x)=1
View SolutionFind the image of the point (1,3,4) in the plane 2x−y+z+3=0.
View SolutionFind the ratio in which the line segment joining the points (2,-1,3) and (-1,2,1) is divided by the plane x+y+z=5.
View Solutionthen image of the point (-1,3,4) in the plane x-2y=0
View SolutionAssertion: The point A(3,1,6) is the mirror image of the point B(1,3,4) in the plane x−y+z=5. Reason: The plane x−y+z=5 bisects the line segment joining A(3,1,6)andB(1,3,4) (A) Both A and R are true and R is the correct explanation of A (B) Both A and R are true R is not the correct explanation of A (C) A is true but R is false. (D) A is false but R is true.
View SolutionAsertion: The point A(3,1,6) is the mirror image of the point B(1,3,4) in the plane x−y+z=5. Reason: The plane x−y+z=5 bisects he segment joining A(3,1,6) and B(1,3,4). (A) Both A and R are true and R is the correct explanation of A (B) Both A and R are true R is not te correct explanation of A (C) A is true but R is false. (D) A is false but R is true.
View SolutionFind the image of the point (1,3,4) in the plane 2x−y+z+3=0.
View Solutionप्रकथन-1 : तल x−y+z=5 में बिन्दु B(1, 3, 4) का दर्पण प्रतिबिम्ब बिन्दु A(3, 1, 6) है।
प्रकथन-2 : तल x-y+z= 5, A(3, 1, 6) तथा B(1, 3, 4) को मिलाने वाले रेखाखण्ड को समद्विभाजित करता है।
View Solutionबिंदुओं (5,-1,4) तथा (4,-1,3) को मिलाने वाले रेखाखण्ड का समतल x+y+z=7 पर डाले गए प्रक्षेप की लम्बाई है: (i) 13 (ii) √23 (iii) 2√3 (iv) 23
View SolutionStatement I - Floor x-y+z=5 Point in B(1, 3, 4) Mirror image of A(3,1,6) is. Statement II - Floor x-y+z=5, A(3,1,6) And B(1, 3,4) Bisects the line segment joining to.
View SolutionFind the image of the point (1,3,4) in the plane 2x-y +z = -3.
View Solutionfind the equation to the plane passing through the line x=y=z and the point (-1,3,4).
View SolutionAssertion: The point A(3,1,6) is the mirror image of the point B(1,3,4) in the plane x−y+z=5. Reason: The plane x−y+z=5 bisects the line segment joining A(3,1,6)andB(1,3,4) (A) Both A and R are true and R is the correct explanation of A (B) Both A and R are true R is not the correct explanation of A (C) A is true but R is false. (D) A is false but R is true.
View SolutionAsertion: The point A(3,1,6) is the mirror image of the point B(1,3,4) in the plane x−y+z=5. Reason: The plane x−y+z=5 bisects he segment joining A(3,1,6) and B(1,3,4). (A) Both A and R are true and R is the correct explanation of A (B) Both A and R are true R is not te correct explanation of A (C) A is true but R is false. (D) A is false but R is true.
View Solution

