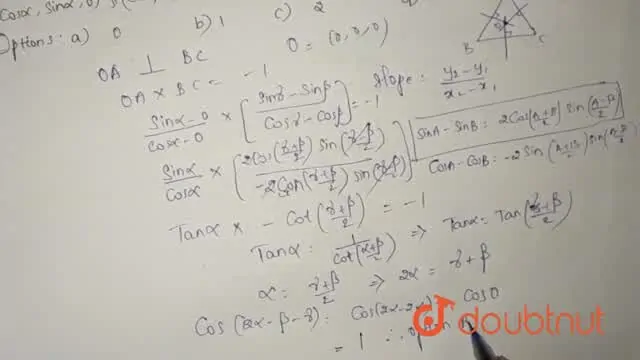If origin is the orthocentre of a triangle formed bythe points (cosα,sinα,0),(cosβ,sinβ,0),(cosγ,sinγ,0) then ∑cos(2α−β−γ)= -Solution in Telugu
0
1
2
3
The correct Answer is:D
Step by step video, text & image solution for If origin is the orthocentre of a triangle formed bythe points (cos alpha, sin alpha,0), (cos beta, sin beta,0), (cos gamma, sin gamma,0) then sumcos(2alpha-beta-gamma)= - by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - COORDINATE SYSTEM (2D) EXERCISE - EXERCISE 971videos
COORDINATE SYSTEM (2D)
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - COORDINATE SYSTEM (2D) EXERCISE - EXERCISE 981videos
COORDINATE SYSTEM (2D)
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - COORDINATE SYSTEM (2D) EXERCISE - EXERCISE 951videos
COORDINATE SYSTEM (2D)
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - COMPLEX NUMBERS EXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) (SET - 4)5videos
COMPLEX NUMBERS
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - COORDINATE SYSTEM (3D)EXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) (SET- 4)3videos
COORDINATE SYSTEM (3D)
Similar Questions
If A(3, -4), B(7, 2) are the ends of a diameter of a circle and C(3, 2) is a point on the circle, then the orthocentre of the ΔABC is
02:37View SolutionThe incentre of the triangle formed by the points (0, 0), (5, 12), (16, 12) is
07:34View SolutionIf O is the orthocentre of the triangle formed by A(1, -3), B(7, 2), C(2, 5) then the distance between the orthocentres of ΔBOC,ΔAOB is
06:24View SolutionA : If argument of z1=π/3 , argument of z2=π/4 then argument of z1z2 is 7π/12
R : Arg (z1z2)=Argz1+Argz202:15View SolutionA: The distance of the (1,2,3) from the coordinate axes are √13,√10,√5
R : The distance of P (x,y,z) from the coordinate are √y2+z2,√x2+z2,√x2+y206:25View Solutionsin alpha, cos alpha, cos (alpha + delta) sin beta, cos beta, cos (beta + delta) sin gamma, cos gamma, cos (gamma + delta)] | = 0
05:29View SolutionIf cos(α−β)+cos(β−γ)+cos(γ−α)=−32 , prove that cosα+cosβ+cosγ=sinα+sinβ+sinγ=0
09:01View SolutionIf cos alpha+cos beta+cos gamma=0 and also sin alpha+sin beta+sin gamma=0 then prove that
10:49View SolutionProve that det [[sin alpha, cos alpha, sin (alpha + delta) sin beta, cos beta, sin (beta + delta) sin gamma, cos gamma, sin (gamma + delta)]] = 0
07:17View SolutionIf origin is the orthocenter of a triangle formed by the points (cos alpha*sin alpha,0)*(cos beta,sin beta.0),(cos gamma,sin gamma,0) then sum cos(2 alpha-beta-gamma)=
05:31View SolutionThe orthocentre of triangle formed by (a cos alpha,a sin alpha),(a cos beta,a sin beta),(a cos gamma,a sin gamma) is
05:16View SolutionIf cosα+cosβ+cosγ=0
=sinα+sinβ+sinγ then show that
cos3α+cos3β+cos3γ=3cos(α+β+γ)07:17View SolutionIf cosα+cosβ+cosγ=0
=sinα+sinβ+sinγ then show that
sin3α+sin3β+sin3γ=3sin(α+β+γ)04:08View SolutionIf cosα+cosβ+cosγ=0
=sinα+sinβ+sinγ then show that
cos(α+β)+cos(β+γ)+cos(γ+α)=0View Solutionयदि cos(β−γ)+cos(γ−α)+cos(α−β)=−32, तो सिद्ध करें की cosα+cosβ+cosγ=0,sinα+sinθ+sinγ=0
04:33View SolutionIf A=(cosα,sinα,0),B=(cosβ,sinβ,0),C=(cosγ,sinγ,0) are vertices of ΔABC and cosα+cosβ+cosγ=3a,sinα+sinβ+sinγ=3b then orthocentre is
02:44View Solution